反转栈 ☆☆
采用 递归 的方式逆序输出栈的数据,不能使用其它数据结构
/**
* 《程序员代码面试指南》 仅使用递归的方式反转一个栈
*
* @author ychost
* @date 2018-1-30
*/
@Data
public class StackReverseByRecursive {
/**
* 取出出栈底元素
*
* @param stack
* @param <T>
* @return
*/
static <T> T pollBottom(Stack<T> stack) {
var data = stack.pop();
if (stack.isEmpty()) {
return data;
} else {
//last 为 「栈底」元素
var last = pollBottom(stack);
//data 为 「栈底」之上的元素
stack.push(data);
return last;
}
}
/**
* 反转一个栈
*
* @param stack
* @param <T>
*/
static <T> void reverse(Stack<T> stack) {
if (stack.isEmpty()) {
return;
}
//将栈底元素一个一个取出来
var data = pollBottom(stack);
reverse(stack);
//第一个放入的就是最后一次取出的「栈底」,即 「栈顶」元素
//从而实现了反转
stack.push(data);
}
}
最大子矩阵 ☆☆☆
给定一个只有 0 和 1 两种元素的矩阵,求全是 1 元素的矩形区域中的最大矩形区域的 1 的个数。
如:
\(\begin{Bmatrix}
1 & 0 & 1 & 1 \\
1 & 1 & 1 & 1 \\
1 & 1 & 1 & 0 \\
\end{Bmatrix}\)
其中,最大矩形区域有 6 个 1,所以结果为 6
思路:
将题目稍作转换,以矩阵的每一行的索引作为横坐标,包括该行在内到第 1 行中连续 1 的个数作为纵坐标,则求出这样的直方图中的扩展的最大矩形区域的面积,
如:
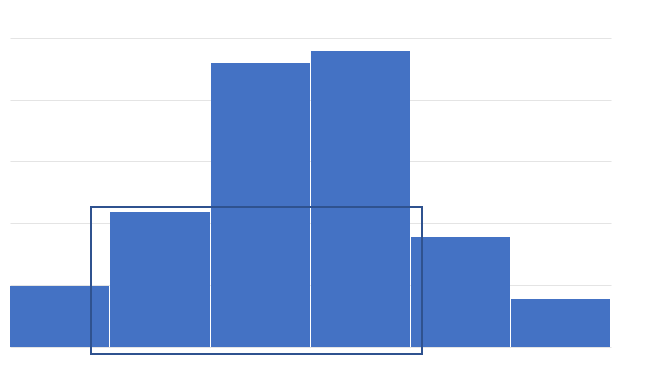
图中第二个元素所能扩展的最大矩形区域面积如上图所示,求出所有这样扩展的矩形区域面积然后取最大值,就能得到本题的解。
具体算法如下:
- 将矩阵的每一行为单位进行转换到如上所述的直方图数组令为 \(height\),定义一个栈令为 \(stack\)。
- 遍历 \(height\)中的元素(索引为 \(i\)),当\(height[i] <= height[stack.peek()]\),则将\(stack\)顶部元素弹出求其扩展矩形区域的最大面积,否则\(stack.push(i)\)
- 对于弹出元素\(j\)求其最大矩形区域面积公式如下:
\[(i - k - 1)*height[j]\]
其中:\(i\)为待压入的元素的索引,\(k\)为\(stack\)中与\(j\)的相邻元素,\(j\)为弹出元素
特别地:\(j\)为栈底元素,则\(k = -1\),\(j\)为\(height\)中的最后元素则\(i = height.length\)
对于最大矩形区域面积公式证明如下:
- 由\(stack\)中元素的插入规律可知,弹出元素\(j\)向左只能扩展到\(k+1\)的位置,向右只能扩展到\(i\)的位置。
- 可知区域面积的横坐标长度\(i-(k+1) = i-k-1\),高度为\(height[j]\)
- 所以面积为: \[(i - k - 1)*height[j]\]
- 对于两个特殊情况
- 当\(j\)为栈底元素的时候,此时无相邻元素,则认为向左不能进行扩展了,向右还是能扩展到\(i\),所以面积为\(i*height[j]\),可认为\(k=-1\)
- 当\(j==height.length -1\),且直接压入了栈中,那么此时栈不为空,但是该栈还有元素没有弹出,所以直接将该栈元素全部弹出,可知栈底到栈顶元素依次递增 那么,对于每个元素向左还是只能扩展到\(k+1\),但是向右可以扩展所有,所以此时的面积为:\((height.length - k -1)*height[j]\),可认为:\(i=height.length\)
实现:
/**
* 输入:
* 一个只有0,1两种元素组成的矩阵
* 输出:
* 一个只含有 1 的最大子矩阵的 1 的个数
*
* @author ychost
* @date 2018-2-12
*/
public class MaxSubmatrix {
/**
* 解题算法
*
* @param matrix 只含有 1,0两种元素组成的矩阵
* @return 只含有1的最大子矩阵中1的个数
*/
static int getMaxSubmatrixArea(int[][] matrix) {
//切割矩阵
var heightArr = cutMatrix(matrix);
var stack = new Stack<Integer>();
var max = 0;
for (var i = 0; i < heightArr.length; i++) {
//获取每行切割高度扩展的最大矩形区域面积
//只有当栈顶元素 < 当前元素 才进行压栈
//否则弹出栈顶元素,并计算其扩展的最大矩形区域面积
for (var j = 0; j < heightArr[i].length; j++) {
var height = heightArr[i];
while (!stack.isEmpty() && height[stack.peek()] >= height[j]) {
var size = popStackGetMaxRecArea(stack, height, j);
max = size > max ? size : max;
}
stack.push(j);
}
while (!stack.isEmpty()) {
var size = popStackGetMaxRecArea(stack, heightArr[i], heightArr[0].length);
max = size > max ? size : max;
}
}
return max;
}
/**
* 从栈中弹出元素,并获取该元素能够扩展的最大矩形区域的面积
*
* @param stack 存有「height 索引」的栈
* @param height 矩阵切割的某行的高度
* @param i 待压如栈顶的元素的索引
* @return 扩展的最大矩形区域面积
*/
static int popStackGetMaxRecArea(Stack<Integer> stack, int[] height, int i) {
var j = stack.pop();
var k = -1;
if (!stack.isEmpty()) {
k = stack.peek();
}
//弹出元素对应的面积
return (i - k - 1) * height[j];
}
/**
* 将矩阵进行切割,找出从第0行到切割行之间连续「1」的个数
*
* @param matrix 矩阵
* @return 连续为「1」的个数为元素的数组
*/
static int[][] cutMatrix(int[][] matrix) {
var heightArr = new int[matrix.length][matrix[0].length];
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
if (i == 0) {
heightArr[i][j] = matrix[i][j];
} else {
heightArr[i][j] = matrix[i][j] == 0 ? 0 : heightArr[i - 1][j] + 1;
}
}
}
return heightArr;
}
}
子数组最值之差 ☆☆☆
给定数组 arr 和整数 num,共返回多少个子数组满足如下情况:
\[ max(arr[i.j]) - min(arr[i..j]) <= num \]
要求:
如果数组的长度为\(N\),请实现时间复杂度为\(o(N)\)的解法
由于要求复杂度为 \(o(N)\),所以就不能暴力的遍历每一个子数组,这里采用两个双端队列来维护 \(arr[i..j]\) 的最大值和最小值的方式。
推论:
- 如果子数组 \(arr[i..j]\) 满足条件,则 \(arr[i..j]\) 的每一个子数组都满足条件,即 \(arr[k..l](i \leq k \leq l \leq l)\) 都满足条件
- 如果子数组 \(arr[i..j]\) 不满足条件,那么 \(arr[k..l](i \leq k \leq l \leq j)\) 都不满足条件
实现:
- 生成两个双端队列
qmax, qmin和两个指针i, j - 令
j++,表示arr[i..j]不断向右扩大,并不断更新qmax, qmin,一旦出现arr[i..j]不满足条件则j停止向右扩大 - 可知移动过程中的
arr[i..j]都是满足条件的,则此次移动共用j - i个子数组满足条件 - 令
i++,不断重复上述过程,直到遍历完整个数组即可求出所有满足条件的子数组的个数 - 上述算法中所有的下标最多进出
qmax, qmin一次,i, j都是不断增加的所以复杂度为 \(o(N)\)
/**
* 给定一数组求其中子数组的最大值减去最小值 <= Num 的子数组数量
* 要求时间复杂度为 o(N)
*
* @author ychost
* @date 2018-2-16
*/
public class MaxSubMinNum {
/**
* 获取子数组中最大值减去最小值 <= num 的子数组的数量
*
* @param arr 待处理数组
* @param num 比较数字
* @return 子数组的数量
*/
static int getSubMinNum(int[] arr, int num) {
var qmax = new LinkedList<Integer>();
var qmin = new LinkedList<Integer>();
var i = 0;
var j = 0;
var res = 0;
while (i < arr.length) {
while (j < arr.length) {
//维护最大值
while (!qmin.isEmpty() && arr[qmin.peekLast()] >= arr[j]) {
qmin.pollLast();
}
qmin.addLast(j);
//维护最小值
while (!qmax.isEmpty() && arr[qmax.pollLast()] <= arr[j]) {
qmax.pollLast();
}
qmax.addLast(j);
//某一 arr[i..j] 不满足情况,停止 j 的扩张
if (arr[qmax.getFirst()] - arr[qmin.getFirst()] > num) {
break;
}
j++;
}
//因为后面有 i++ 所以 arr[i] 已经不能用作最值比较了
if (qmin.peekFirst() == i) {
qmin.pollFirst();
}
if (qmax.peekFirst() == i) {
qmax.pollFirst();
}
//arr[i..j] 的所有子数组都满足
res += j - i;
i++;
}
return res;
}
/**
* 暴力解法,只是用来验证结果
*
* @param arr
* @param num
* @return
*/
static int getSubMinNum2(int[] arr, int num) {
int res = 0;
for (int i = 0; i < arr.length; i++) {
for (int j = i; j < arr.length; j++) {
int max = i;
int min = i;
for (int k = i; k <= j; k++) {
if (arr[k] > arr[max]) {
max = k;
}
if (arr[k] < arr[min]) {
min = k;
}
}
if (arr[max] - arr[min] <= num) {
res++;
}
}
}
return res;
}
}