程序员代码面试指南链表

环形单链表的约瑟夫问题 ☆☆☆

从头节点开始报数 1 ，下一个节点报数 2…，当报数为 m 的时候删除该节点，然后下一个节点继续报数 1…，求最后存活下来的节点
输入：一个环形单向链表的头结点 head 和报数的值 m
输出：最后存活下来的节点，且这个节点自己组成环形单链表，其它节点都删除要求：如果链表的节点数为 \(N\)，要求时间复杂度为 \(o(N)\)

思路：
在不考虑时间复杂度的情况可以进行暴力求解，即循环遍历环型链表然后将报数为 m 的节点删除，最后只剩下一个节点的时候即为所求的存活的节点
当考虑到时间复杂度 \(o(N)\) 的时候就不能用不断遍历求值的方式了，必须一步到位计算出存活节点的编号，即给定链表长度 size 、报数值 m 的时候就能直接求出最后存活节点的编号 n

找到报数值 \(M\) 和节点编号 \(N\) 的关系（头结点编号为 1，下一个节点为 2 …，链表的长度为 \(L\)，不考虑删除节点）

M	N
1	1
2	2
..	..
L	L
L+1	1
L+2	2
..	..

不难看出 \(M\), \(N\), \(L\) 之间的关系
\[N = (M-1) \% L + 1 \]

在删除节点的情况下，找到长度为 \(L\) 的时候存活节点与长度为 \(L-1\) 的存活节点之间的关系（令删除的节点为 \(s\)）

L	L-1
..	..
s-2	L-2
s-1	L-1
s	已经被删除了
s+1	1
s+2	2
..	..

不难看出，在长度为 \(L\) 的报数 \(f(L)\)，与 \(L-1\)的报数 \(f(L-1)\) 之间的关系 \[f(L)= (f(L-1)+ s -1) \% L + 1\] 令报数到 \(x\) 的被删掉，则被删的节点编号为： \[s = (x -1) \% L + 1\] 可得：
\[f(L) = (f(L-1) + (x - 1)\% L) \%L +1\] 可知，上面的关系式为一个递推的关系式，特别地，如果 \(L == 1\)，那么存活的节点也为 \(1\) 在 \(o(N)\) 的时间内直接获得存活节点的代码如下

    /**
     * 使用递归的方式直接获取约瑟夫问题中存活的节点编号
     *
     * @param size 单向链的长度
     * @param num  报数
     * @return 唯一存活的节点编号
     */
    static int getAliveNum(int size, int num) {
        if (size == 1) {
            return 1;
        }
        //长度为 size 与 (size-1) 存活节点编号的关系
        return (getAliveNum(size - 1, num) + (num - 1) % size) % size + 1;
    }

附完整代码：

/**
 * 环形单链表的约瑟夫问题
 *
 * @author ychost
 * @date 2018-2-24
 */
public class LinkedListJosephus {
    /**
     * 获取存活下来的节点
     *
     * @param header 链表头部指针
     * @param num    报数值
     * @return 没有报到该数，即存活下来的节点
     */
    static OneWayNode getAliveNode(OneWayNode header, int num) {
        var pointer = header;
        //形成环状
        //如果 header 所在链表已是环状则找到 header 的 previous
        while (pointer.getNext() != null && pointer.getNext() != header) {
            pointer = pointer.getNext();
        }
        pointer.setNext(header);
        //尾指针
        OneWayNode previous = pointer;
        //头指针
        pointer = header;
        int i = 0;
        while (pointer != pointer.getNext()) {
            //删除报数到 num 的节点
            if (++i % num == 0) {
                previous.setNext(pointer.getNext());
            }
            previous = pointer;
            pointer = pointer.getNext();
        }
        return pointer;
    }


    /**
     * 另一种高效的方法，在 o(N) 的时间内完成
     *
     * @param header
     * @param num
     * @return
     */
    static OneWayNode getAliveNode2(OneWayNode header, int num) {
        var pointer = header;
        //获取链表的长度
        var size = 1;
        while (pointer.getNext() != null && pointer.getNext() != header) {
            size++;
            pointer = pointer.getNext();
        }
        pointer = header;
        var aliveNum = getAliveNum(size, num);
        while (--aliveNum != 0) {
            pointer = pointer.getNext();
        }
        pointer.setNext(pointer);
        return pointer;
    }

    /**
     * 使用递归的方式直接获取约瑟夫问题中存活的节点编号
     *
     * @param size 单向链的长度
     * @param num  报数
     * @return 唯一存活的节点编号
     */
    static int getAliveNum(int size, int num) {
        if (size == 1) {
            return 1;
        }
        //长度为 size 与 (size-1) 存活节点编号的关系
        return (getAliveNum(size - 1, num) + (num - 1) % size) % size + 1;
    }
}

判断一个链表是否为回文 ☆☆☆

给定一个链表的头部节点，判断链表是否为回文，例如：
1->2->1 是回文
1->2->2->1 是回文
1->3->3->2 不是回文
如果链表长度为 \(N\)，要求时间复杂度为 o(N)，空间复杂度为 \(o(1)\)

思路：
在不考虑空间复杂度的情况下，利用栈可以简单实现回文的判断，即出栈的顺序就为链表的反序遍历。
考虑到空间复杂度，可以将链表从中间分作两部分，将右半部分进行反转，如果结果和左半部分相等，则为回文，最后再将链表恢复即可。

/**
 * 判断链表是否是一个回文
 *
 * @author ychost
 * @date 2018-2-26
 */
public class LinkedListIsPalindrome {
    /**
     * 判断是否为回文的普通解法
     *
     * @param header 单向链表的头指针
     * @return 判断结果
     */
    static boolean isPalindrome(OneWayNode header) {
        var stack = new Stack<Object>();
        var pointer = header;
        while (pointer != null) {
            stack.push(pointer.getData());
            pointer = pointer.getNext();
        }
        pointer = header;
        while (!stack.isEmpty()) {
            if (!pointer.getData().equals(stack.pop())) {
                return false;
            }
            pointer = pointer.getNext();
        }
        return true;
    }

    /**
     * 另一种高效解法，时间效率为 o(N)，空间效率为 o(1)
     * 该方法为反转链表右半部分，然后左半部分遍历的结果应该等于右半部分
     *
     * @param header 单向链表的头指针
     * @return 判断结果
     */
    static boolean isPalindrome2(OneWayNode header) {
        OneWayNode n1, n2, n3;
        n1 = header;
        n2 = header;
        //使得 n1 指向链表的中间节点
        while (n2.getNext() != null && n2.getNext().getNext() != null) {
            n1 = n1.getNext();
            n2 = n2.getNext().getNext();
        }
        n2 = n1.getNext();
        n1.setNext(null);
        //反转链表的右半部分
        while (n2 != null) {
            n3 = n2.getNext();
            n2.setNext(n1);
            n1 = n2;
            n2 = n3;
        }
        n3 = n1;
        n2 = header;
        var res = true;
        //此时 n1 指向右反转链表的第一个节点，n2 指向左链表的第一个节点
        while (n1 != null && n2 != null) {
            if (!n1.getData().equals(n2.getData())) {
                res = false;
                break;
            }
            n1 = n1.getNext();
            n2 = n2.getNext();
        }
        //恢复链表
        n1 = n3.getNext();
        n3.setNext(null);
        //此时 n1 指向原链表的尾节点
        while (n1 != null) {
            n2 = n1.getNext();
            n1.setNext(n3);
            n3 = n1;
            n1 = n2;
        }
        return res;

    }
}

复制含有随机指针节点的链表 ☆☆

复制如下数据结构的链表，要求时间复杂度 \(o(N)\)，只能使用几个变量

/**
 * 比普通的单向链表多了一个随机指针
 *
 * @param <T>
 */
@Data
class RandNode<T>  {
    private T data;
    private RandNode<T> next;
    private RandNode<T> rand;


    RandNode(T data) {
        this.data = data;
    }

    @Override
    public int hashCode() {
        return this.data.hashCode();
    }
}

思路：

在不考虑空间复杂度的情况可以使用HashMap来保存原节点和复制节点，然后遍历原节点从HashMap中取出复制节点即可。
考虑空间复杂度的情况下，可以将复制节点直接追加到原节点后面比如原节点为：
```
 1->2->3->4->null
```
复制后的链表如下：
```
 1->1'->2->2'->3->3'->null
```
那么 node1.getRande() 的复制节点就为 node1.getRande().getNext()

实现：

/**
 * 复制 RandNode 这样的链表
 *
 * @author ychost
 * @date 2018-2-28
 */
public class LinkedListCopyRandNode {
    /**
     * 复制链表，使用 HashMap 来保存复制对应关系
     *
     * @param header 待复制链表的头指针
     * @return 复制后的链表的头指针
     */
    static RandNode<Integer> copy(RandNode<Integer> header) {
        RandNode<Integer> copyHeader = null, copyPointer = null;
        var map = new HashMap<RandNode<Integer>, RandNode<Integer>>();
        var pointer = header;
        //复制 next 连接
        while (pointer != null) {
            //复制对应关系
            if (!map.containsKey(pointer)) {
                var node = new RandNode<Integer>(pointer.getData());
                map.put(pointer, node);
            }
            if (!map.containsKey(pointer.getRand())) {
                if (pointer.getRand() != null) {
                    var node = new RandNode<Integer>(pointer.getRand().getData());
                    map.put(pointer.getRand(), node);
                }
            }
            //关联关系对象
            RandNode<Integer> copyNode = map.get(pointer);
            if (copyPointer == null) {
                copyHeader = copyNode;
            } else {
                copyPointer.setNext(copyNode);
            }
            copyPointer = copyNode;
            copyPointer.setRand(map.get(pointer.getRand()));

            pointer = pointer.getNext();
        }
        return copyHeader;
    }

    /**
     * 另一种高效的做法，时间复杂度 o(N)，只使用几个临时变量
     * 创建这样的数据结构 1-1'-2-2'...
     * 将复制的节点保存在原节点后面，然后寻找复制 rand 节点就在圆 rand 节点后面
     *
     * @param header
     * @return
     */
    static RandNode<Integer> copyEff(RandNode<Integer> header) {
        var pointer = header;
        RandNode<Integer> next = null;
        //复制节点
        while (pointer != null) {
            next = pointer.getNext();
            var copy = new RandNode<Integer>(pointer.getData());
            pointer.setNext(copy);
            copy.setNext(next);
            pointer = next;
        }
        //连接 rand 节点
        pointer = header;
        while (pointer != null && pointer.getNext() != null) {
            if (pointer.getRand() != null) {
                var copyRand = pointer.getRand().getNext();
                var copyNode = pointer.getNext();
                copyNode.setRand(copyRand);
            }
            pointer = pointer.getNext().getNext();
        }

        RandNode<Integer> copyHeader = null, copyPointer = null;
        pointer = header;
        //取出复制的链表
        while (pointer != null) {
            var copyNode = pointer.getNext();
            if (copyPointer == null) {
                copyHeader = copyNode;
            } else {
                copyPointer.setNext(copyNode);
            }
            copyPointer = copyNode;
            var orgNext = pointer.getNext().getNext();
            pointer.setNext(orgNext);
            pointer = orgNext;
        }
        return copyHeader;
    }
}

附：测试代码

    @Test
    public void copy() {
        var header = new RandNode<Integer>(0);
        var pointer = header;
        var nodeArr = (RandNode<Integer>[]) new RandNode[10];
        for (int i = 0; i < nodeArr.length; i++) {
            nodeArr[i] = new RandNode<>(i + 1);
            pointer.setNext(nodeArr[i]);
            pointer = nodeArr[i];
        }
        //数组洗牌
        var r = new Random();
        for (int i = nodeArr.length - 1; i >= 1; i--) {
            int j = r.nextInt(i);
            var t = nodeArr[i];
            nodeArr[i] = nodeArr[j];
            nodeArr[j] = t;
        }
        //设置随机连接
        header.setRand(nodeArr[0]);
        for (int i = 0; i < nodeArr.length - 1; i++) {
            nodeArr[i].setRand(nodeArr[i + 1]);
        }
        var copyPointer = LinkedListCopyRandNode.copyEff(header);
        pointer = header;
        //校验
        while (copyPointer != null) {
            Assert.assertEquals(pointer.getData(), copyPointer.getData());
            Assert.assertNotEquals(pointer, copyPointer);

            if (pointer.getRand() != null) {
                Assert.assertEquals(pointer.getRand().getData(), copyPointer.getRand().getData());
                Assert.assertNotEquals(pointer.getRand(), copyPointer.getRand());
            }
            copyPointer = copyPointer.getNext();
            pointer = pointer.getNext();
        }
    }

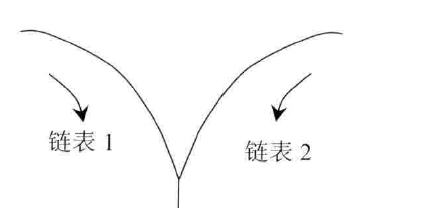
两个链表的相交问题 ☆☆☆☆☆

要求：
时间负责度 \(o(M+N)\)，空间复杂度 \(o(1)\)

1. 两个无环链表相交

若相交则必有公共的尾节点，相同长度的相交部分
较长的链表先走两个链表长度之差
两个链表再同时走必然会相遇，相遇点即为第一个相交点

     /**
     * header1->end1 链表和 header2->end2 链表之间的第一个交点
     *
     * @param header1 链表1头指针
     * @param header2 链表2头指针
     * @param end1    链表1 tail.next
     * @param end2    链表2 tail.next
     * @return 第一个相交点
     */
    static OneWayNode getNoLoopIntersect(OneWayNode header1, OneWayNode header2,
                                             OneWayNode end1, OneWayNode end2) {
        //获取两个链表的长度和尾结点
        OneWayNode pointer = header1;
        int len1 = 1, len2 = 1;
        while (pointer.getNext() != end1) {
            pointer = pointer.getNext();
            ++len1;
        }
        end1 = pointer;
        pointer = header2;
        while (pointer.getNext() != end2) {
            pointer = pointer.getNext();
            ++len2;
        }
        end2 = pointer;
        //如果两个链表有交点，则尾结点必定一致
        if (end1 != end2) {
            return null;
        }
        var diff = Math.abs(len1 - len2);
        var pLong = len1 > len2 ? header1 : header2;
        var pShort = pLong == header1 ? header2 : header1;
        //两个链表剩余的长度一致
        while ((diff--) > 0) {
            pLong = pLong.getNext();
        }
        //在长度一致的情况下必然相遇点为交点
        while (pLong != pShort) {
            pLong = pLong.getNext();
            pShort = pShort.getNext();
        }
        return pLong;
    }

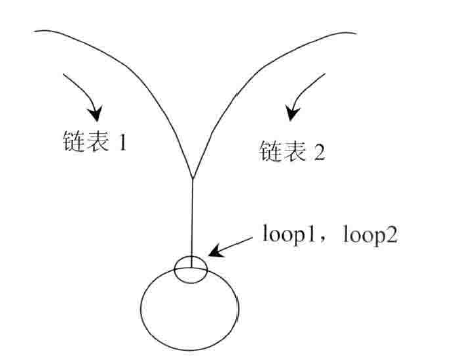
2. 两个有环链表相交

如果一个链表有环，一个链表无环，则必不想交
情况1：两个链表在入环之前相交
该情况和两个无环链表相交的情况类似，只是无环链表的 end 是 null，此时的 end 为 loopNode.next
情况2：两个链表的相交点在环内
该情况如下面两种情形
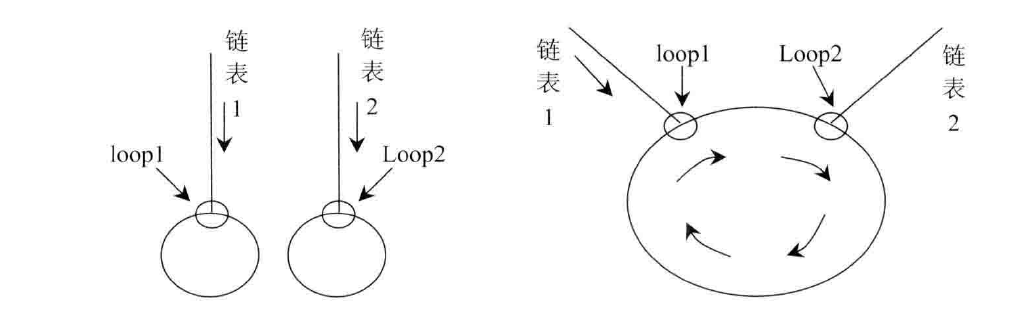
左图为不相交情形，右图为相交情形
如果 loop1 遍历环一周没有遇见 loop2 则不想交，否则相交，此时返回 loop1 和 loop2 均可

loop1 是离链表1较近的相交点，loop2 是离链表2较近的相交点

    /**
     * 获取两个有环链表的交点
     *
     * @param header1 有环表
     * @param header2 有环表
     * @return
     */
    static OneWayNode getLoopIntersect(OneWayNode header1, OneWayNode header2) {
        var loop1 = getLoopNode(header1);
        var loop2 = getLoopNode(header2);
        //如果一个链表有环，另一个链表无环
        //则必然不相交
        var noIntersect = loop1 == null ? loop2 != null : loop2 == null;
        if (noIntersect) {
            return null;
        }
        //两个链表共用一个入环点，则交点在入环点之前
        //则可视作为 header1->loop1，header2->loop2 之间的无环表的交点
        if (loop1 == loop2) {
            return getNoLoopIntersect(header1, header2, loop1.getNext(), loop2.getNext());
            //两个链表的入环点不一样
        } else {
            var pointer = loop2.getNext();
            while (pointer != loop1 && pointer != loop2) {
                pointer = pointer.getNext();
            }
            //只有两个链表入一个环才有交点
            //此时返回 loop1，loop2 都可以
            if (pointer == loop1) {
                return loop1;
            }
        }
        return null;
    }

    /**
     * 若链表有环则第一个入环节点
     * 采用 Fast/Slow Runner 算法
     *
     * @param header 链表头部指针
     * @return 入环节点，如果无环则返回 null
     */
    static OneWayNode getLoopNode(OneWayNode header) {
        var faster = header;
        var slower = header;
        //若有环两个指针必然相遇
        while (faster != null && faster.getNext() != null) {
            slower = slower.getNext();
            faster = faster.getNext().getNext();
            if (faster == slower) {
                break;
            }
        }
        if (faster != slower) {
            return null;
        }
        //置位 faster，下次相遇节点即为入环点
        faster = header;
        while (faster != slower) {
            faster = faster.getNext();
            slower = slower.getNext();
        }
        return slower;
    }

3. 附代码

 /**
     * 获取两个链表的第一个相交点，如果不相交则返回 null
     * 要求时间复杂度 o(M+N)，空间复杂度 o(1)
     *
     * @param header1 链表1，可能有环
     * @param header2 链表2，可能有环
     * @return 相交点
     */
    static OneWayNode getIntersectPoint(OneWayNode header1, OneWayNode header2) {
        var loop1 = getLoopNode(header1);
        var loop2 = getLoopNode(header2);
        if (loop1 == null && loop2 == null) {
            return getNoLoopIntersect(header1, header2, null, null);
        } else if (loop1 != null && loop2 != null) {
            return getLoopIntersect(header1, header2);
        }
        return null;
    }

夏天

程序员代码面试指南链表

环形单链表的约瑟夫问题 ☆☆☆

判断一个链表是否为回文 ☆☆☆

复制含有随机指针节点的链表 ☆☆

两个链表的相交问题 ☆☆☆☆☆

1. 两个无环链表相交

2. 两个有环链表相交

情况1：两个链表在入环之前相交

情况2：两个链表的相交点在环内

3. 附代码

搜索

文章目录

程序员代码面试指南 链表

环形单链表的约瑟夫问题 ☆☆☆

判断一个链表是否为回文 ☆☆☆

复制含有随机指针节点的链表 ☆☆

两个链表的相交问题 ☆☆☆☆☆

1. 两个无环链表相交

2. 两个有环链表相交

情况1：两个链表在入环之前相交

情况2：两个链表的相交点在环内

3. 附代码

搜索

文章目录

程序员代码面试指南链表