题目
编辑距离,又称 Levenshtein 距离(也叫做 E Distance),是指两个字串之间,由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。
例如将 kitten 一字转成 sitting:
sitten (k-<s)
sittin (e-<i)
sitting (-<g)
所以 kitten 和 sitting 的编辑距离是 3。俄罗斯科学家 Vladimir Levenshtein 在 1965 年提出这个概念
思路
- 这也是个求最优解的问题,考虑使用动态规划
- 状态描述:E(i,j) 表示 fs[0..i] 到 ts[0..j] 的编辑距离,即求 E(m,n)
fs字符串 需要编辑到 ts 字符串 m 为 fs 的长度,n 为 ts 的长度
可知:
- E(0,j)=j
表示 fs[0..0] 到 ts[0..j] 的编辑距离,由于 fs 为空串,所以编辑距离为 j(插入 ts[0..j] 的字符即可)
- E(i,0)=i
表示 fs[0..i] 变成空串
- 若E(i-1,j) + 1 = E(i,j) 则表示经过了 Insert
fs[0..i-1] –> fs[0..i] 很明显长度增加了一个单位
- 若E(i,j-1) +1 = E(i,j) 则表示经过了 Delete, 即
相当于 fs(i) 无效,因为有了 fs(i) 反而编辑距离减少到 ts(j-1),所以需要删掉 fs(i)
- 若E(i-1,j-1) + 1= E(i,j) 则表示经过了 Change
从 i-1 到 i 的状态没有字符长度的变更,所以只能是对某位进行了修改。
-
综上: \(E(i,j)=\begin{cases} j & i=0 \\ i & j=0 \\ min \begin{cases} E(i-1,j)+1 & \text{Insert} \\ E(i,j-1)+1 & \text{Delete} \\ E(i-1,j-1)+f & \text{Change} \end{cases}\\ \end{cases}\)
其中, \(f = \begin{cases} 0, & fs[i]=ts[j] \\ 1, & fs[i]!=ts[j] \end{cases}\)
实现
/**
* 求两个字符串的编辑距离
*
* @author ychost
* @date 2018-3-14
*/
public class EDistance {
/**
* 将 fromStr 变成 toStr 所需要的编辑次数
* 编辑只有:插入、修改、删除一个字符
*/
static int getDistance(String fromStr, String toStr) {
int[][] dp = new int[fromStr.length() + 1][toStr.length() + 1];
for (int i = 0; i <= fromStr.length(); i++) {
dp[i][0] = i;
}
for (int j = 0; j <= toStr.length(); j++) {
dp[0][j] = j;
}
for (int i = 1; i <= fromStr.length(); i++) {
for (int j = 1; j <= toStr.length(); j++) {
//添加操作
int insert = dp[i - 1][j] + 1;
//删除
int remove = dp[i][j - 1] + 1;
//修改字符
int change = dp[i - 1][j - 1] + (fromStr.charAt(i - 1) == toStr.charAt(i - 1) ? 0 : 1);
dp[i][j] = min(insert, remove, change);
}
}
return dp[fromStr.length()][toStr.length()];
}
static int min(int... rest) {
int min = rest[0];
for (int e : rest) {
min = Math.min(e, min);
}
return min;
}
}
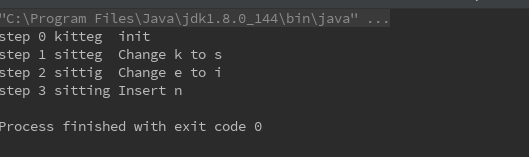
打印出修改的过程:
从 E[i][j] 与上一步 E[i-1][j], E[i][j-1], E[i-1][j-1] 之间比较就能反推出,上一个状态到下一个状态发生了什么
然后通过栈来存操作指令,最后出栈的时候就是从第一个状态到最后状态的指令数据
而每一步指令所对应的结果可以通过对 toStr 反向操作获取
static void print(int[][] edit, String fromStr, String toStr) {
int i = edit.length - 1, j = edit[0].length - 1;
StringBuilder builder = new StringBuilder(toStr);
//存放操作步骤
Stack<String> stack = new Stack<>();
stack.push(toStr);
//对于 builder 而言,相当于是 toStr 到 fromStr 的一个过程
// 所以动作和实际动作相反
while (i > 0 || j > 0) {
String str = null;
if (i != 0 && j != 0) {
if (edit[i][j] == edit[i - 1][j - 1]) {
i -= 1;
j -= 1;
continue;
} else if (edit[i][j] == edit[i][j - 1] + 1) {
str = "Insert " + toStr.charAt(--j);
builder.deleteCharAt(j);
} else if (edit[i][j] == edit[i - 1][j] + 1) {
str = "Del " + fromStr.charAt(--i);
builder.append(fromStr.charAt(i));
} else if (edit[i][j] == edit[i - 1][j - 1] + 1) {
str = "Change " + fromStr.charAt(--i) + " to " + toStr.charAt(--j);
builder.setCharAt(j, fromStr.charAt(i));
} else {
throw new RuntimeException("传入 edit[][] 有误");
}
} else if (i == 0) {
str = "Insert " + toStr.charAt(--j);
builder.deleteCharAt(j);
} else if (j == 0) {
str = "Delete " + fromStr.charAt(--i);
builder.append(fromStr.charAt(i));
}
stack.push(str);
stack.push(builder.toString());
}
//美化输出
int spaceLen = Math.max(fromStr.length(), toStr.length()) + 1;
int index = 0;
//操作指令
String cmd = "init";
//操作结果
String result = stack.pop();
int len = spaceLen - result.length();
//第一行输出 默认值
System.out.println("step " + (index++) + " " + result + String.join("", Collections.nCopies(len, " ")) + cmd);
while (!stack.isEmpty()) {
cmd = stack.pop();
result = stack.pop();
len = spaceLen - result.length();
System.out.println("step " + (index++) + " " + result + String.join("", Collections.nCopies(len, " ")) + cmd);
}
}