算法-堆排序

算法可视化连接
本文的所有操作都是针对的最小堆，对于最大堆的操作也是一样的，唯一的区别就是 shiftdown 和 shiftup 里面的交换规则相反。
本文的图片来源于啊哈磊
复杂度
- 时间复杂度，平均： \(o(nlogn)\)，最好：\(o(nlogn)\)，最坏：\(o(nlogn)\)
- 空间复杂度：\(o(1)\)
- 稳定性：不稳定
  因为堆排序的过程中经常会将元素的相对位置通过向上、向下调整而改变，故不稳定
应用
- 排序
- 求第 k 大或者第 k 小数

背景

堆

这里的堆和内存空间的堆不是一个概念，这里指的是数据结构。
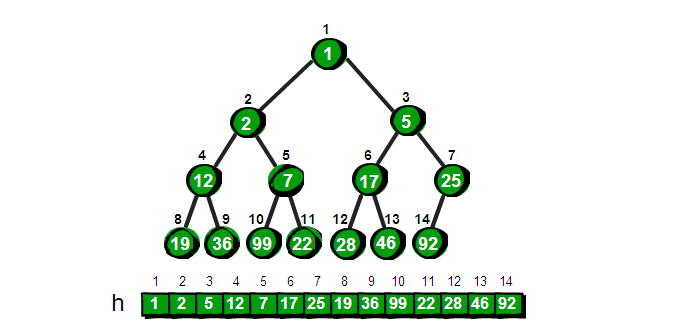
堆在逻辑结构上是一个完全二叉树，物理存储上是数组（完全二叉树父节点和子节点序号存在关系）。
注意完全二叉树和满二叉树的区别，全二叉树最后一层可以不满，详情百度。

因为父子节点存在关系，所以堆可以用数组的形式来表示，关系如下：
左子节点：\(n_l = 2 \times n\)
右子节点：\(n_r = 2 \times n + 1\)

利用向下取整可以得出：
父亲节点：\(n = n'/2\)
\(n'\)为左子节点、右子节点索引都可以

注：本文中的代码的索引是从 0 开始的，即堆顶元素的序号为 0 则
左子节点：\(n_l = 2 \times n + 1\)
右子节点：\(n_r = 2 \times n + 2\)
父亲节点：\(n = (n'-1)/2\)

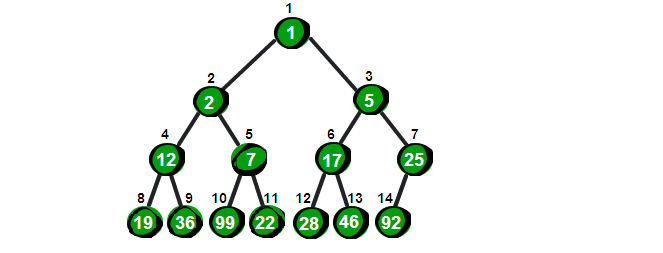
所有的父节点比子节点都要小的堆，当然堆顶元素为最小元素，如图：

反之，所有的父节点都比子节点要大的堆，当然堆顶元素为最大元素。

意义

这种结构有何意义？
对于这种结构，我们可以创建优先队列，比如 PriorityQueue就是基于堆的优先队列，这样我们每次出队的顺序就不是入队的顺序了，而是每次出队都出堆顶元素（最大值或者最小值）达到优先的效果。

基本操作

基本元素

public class HeapSort{
    int[] array;
    int size;
    public HeapSort(int[] array){
        this.array = array;
        this.size = array.length;
    }

    void swap(int i,int j){
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }
}

向上调整

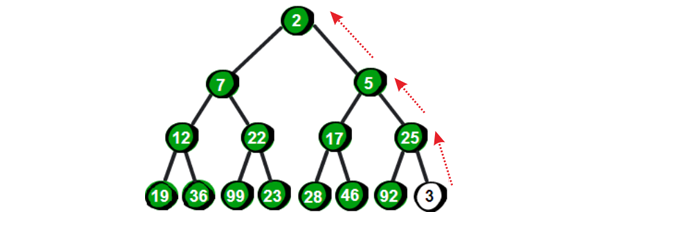
如图，这里添加一个值为 3 的元素到堆尾，然后通过不断的与父元素对比，然后交换，直到满足堆结构位置。
这里是一个最小堆，即交换的终止条件为：data > father，否者一直与father交换下去

   /**
     * 向上调整堆中某个节点
     *
     * @param i 节点在数组中的索引，从 0 开始
     */
    public void shiftUp(int i) {
        if (i <= 0) {
            return;
        }
        int fatherIndex = (i - 1) / 2;
        if (array[fatherIndex] > array[i]) {
            swap(i, fatherIndex);
            shiftUp(fatherIndex);
        }
    }

向下调整

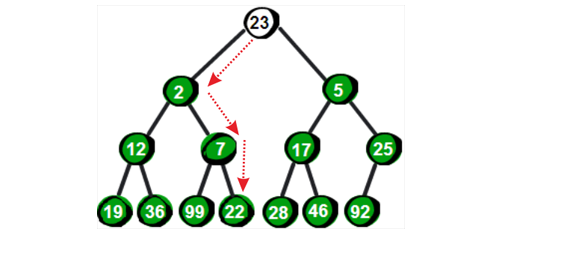
如图，这里将值为 23 的元素向下进行调整，它会一直与自己的左右子节点进行对比，一路交换下去。

交换的终止条件：data < left && data < right，即节点比两个子节点都小的时候。
如果仅有一个子节点满足条件，则与之交换。
如果两个子节点都满足条件，则交换子节点中较小的。

   /**
     * 向下调整堆中某个节点
     *
     * @param i 节点在数组中的索引，从 0 开始
     */
    public void shiftDown(int i) {
        int leftIndex = 2 * i + 1;
        int rightIndex = 2 * i + 2;
        if (leftIndex >= size) {
            return;
        }
        //找到较小的子节点索引
        int minIndex = leftIndex;
        if (rightIndex < size && array[rightIndex] < array[leftIndex]) {
            minIndex = rightIndex;
        }

        //与较小节点进行交换
        if (array[minIndex] < array[i]) {
            swap(i, minIndex);
            //将交换后的节点继续向下调整
            shiftDown(minIndex);
        }
    }

添加元素

将一个元素放入堆尾，然后将该元素 向上调整 以保证堆结构

    /**
     * 添加一个节点，将节点添加到堆尾，然后向上调整该节点
     *
     * @param val 添加节点值
     */
    public void offer(int val) {
        if (size >= array.length) {
            //防止越界
            ensure(size + 1);
        }
        array[size - 1] = val;
        shiftUp(size - 1);
    }

    /**
     * 确保数组不会越界
     *
     * @param len
     */
    private void ensure(int len) {
        if (len <= array.length) {
            return;
        }
        int[] newArr = new int[len];
        for (int i = 0; i < size; i++) {
            newArr[i] = array[i];
        }
        size = len;
        array = newArr;
    }

删除元素

将待删除元素与堆尾元素互换，删除堆尾，然后将交换后的元素 向下调整 以保证堆的结构

    /**
     * 将堆的顶节点弹出
     * 用堆尾元素赋值给堆顶元素，然后移除掉堆尾，再对堆顶元素进行向下调整
     */
    public int poll() {
        int data = array[0];
        array[0] = array[--size];
        shiftDown(0);
        return data;
    }

    /**
     * 删除某个节点元素
     *
     * @param i 节点在数组中的索引
     */
    public void deleteIndex(int i) {
        if (i < 0 || i >= size) {
            return;
        }
        array[i] = array[--size];
        int father = array[(i - 1) / 2];
        if (array[i] > father) {
            shiftDown(i);
        } else if (array[i] < father) {
            shiftUp(i);
        }
    }

构造

将初始元素依次放入堆数组。
从最后一个非叶节点到堆顶节点依次 向下调整。
调整后的数组元素即满足堆结构。

   /**
     * 初始化堆
     */
    private void init() {
        //第一个非叶子节点的索引为 (size-1)/2
        for (int i = (size - 1) / 2; i >= 0; i--) {
            shiftDown(i);
        }
    }

排序

将堆顶元素和堆尾元素交换，然后size-=1，然后向下调整堆顶元素。
不断重复上述动作，直到size==0。
经上述操作的结果，最后的array里面的元素是从大到小排列的。

    /**
     * 将初始化传入的数组排序，排序结果为由大到小
     */
    public void sort() {
        int n = size;
        //没必要对最后一个节点向下调整，最后一个节点必定在数组第一个位置
        while (size > 1) {
            swap(0, size - 1);
            --size;
            shiftDown(0);
        }
        size = n;
    }

完整代码

/**
 * 堆排序，最小堆
 *
 * @author ychost
 * @date 2018-3-29
 */
public class HeapSort {
    int[] array;
    int size;

    public HeapSort(int[] array) {
        this.array = array;
        size = array.length;
        init();
    }

    /**
     * 获取堆元素数组
     *
     * @return
     */
    public int[] toArray() {
        int[] arr = new int[size];
        for (int i = 0; i < size; i++) {
            arr[i] = array[i];
        }
        return arr;
    }


    /**
     * 初始化堆
     */
    private void init() {
        //第一个非叶子节点的索引为 (size-1)/2
        for (int i = (size - 1) / 2; i >= 0; i--) {
            shiftDown(i);
        }
    }

    /**
     * 检查队列是否为空
     *
     * @return
     */
    boolean isEmpty() {
        return size <= 0;
    }

    /**
     * 将初始化传入的数组排序，排序结果为由大到小
     */
    public void sort() {
        int n = size;
        while (size > 1) {
            swap(0, size - 1);
            --size;
            shiftDown(0);
        }
        size = n;
    }


    /**
     * 将堆的顶节点弹出
     * 用堆尾元素赋值给堆顶元素，然后移除掉堆尾，再对堆顶元素进行向下调整
     */
    public int poll() {
        int data = array[0];
        array[0] = array[--size];
        shiftDown(0);
        return data;
    }

    /**
     * 删除某个节点元素
     *
     * @param i 节点在数组中的索引
     */
    public void deleteIndex(int i) {
        if (i < 0 || i >= size) {
            return;
        }
        array[i] = array[--size];
        int father = array[(i - 1) / 2];
        if (array[i] > father) {
            shiftDown(i);
        } else if (array[i] < father) {
            shiftUp(i);
        }
    }

    /**
     * 删除第一个值等于 data 的元素
     *
     * @param data
     */
    public void delteObj(int data) {
        for (int i = 0; i < array.length; i++) {
            if (array[i] == data) {
                deleteIndex(i);
                break;
            }
        }

    }


    /**
     * 添加一个节点，将节点添加到堆尾，然后向上调整该节点
     *
     * @param val 添加节点值
     */
    public void offer(int val) {
        if (size >= array.length) {
            ensure(size + 1);
        }
        array[size - 1] = val;
        shiftUp(size - 1);
    }

    /**
     * 确保数组不会越界
     *
     * @param len
     */
    private void ensure(int len) {
        if (len <= array.length) {
            return;
        }
        int[] newArr = new int[len];
        for (int i = 0; i < size; i++) {
            newArr[i] = array[i];
        }
        size = len;
        array = newArr;
    }

    /**
     * 向下调整堆中某个节点
     *
     * @param i 节点在数组中的索引，从 0 开始
     */
    public void shiftDown(int i) {
        int leftIndex = 2 * i + 1;
        int rightIndex = 2 * i + 2;
        if (leftIndex >= size) {
            return;
        }
        int minIndex = leftIndex;
        if (rightIndex < size && array[rightIndex] < array[leftIndex]) {
            minIndex = rightIndex;
        }

        //与较小节点进行交换
        if (array[minIndex] < array[i]) {
            swap(i, minIndex);
            //将交换后的节点继续向下调整
            shiftDown(minIndex);
        }
    }

    /**
     * 向上调整堆中某个节点
     *
     * @param i 节点在数组中的索引，从 0 开始
     */
    public void shiftUp(int i) {
        if (i <= 0) {
            return;
        }
        int fatherIndex = (i - 1) / 2;
        if (array[fatherIndex] > array[i]) {
            swap(i, fatherIndex);
            shiftUp(fatherIndex);
        }
    }

    /**
     * 交换数组中的两个元素
     *
     * @param i 数组中的第一个索引
     * @param j 数组中的第二个索引
     */
    public void swap(int i, int j) {
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }

}

夏天