题目
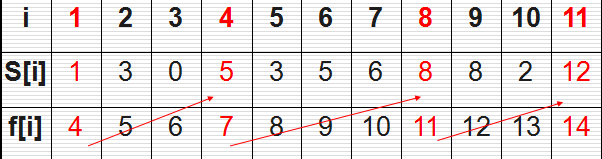
有 n 个需要在同一天使用同一个教室的活动 a1,a2,…,an,教室同一时刻只能有一个活动使用。每个活动 ai 都有一个开始时间si 和结束时间 fi 。一旦被选择后,活动ai就占据时间区[si,fi)。如果 [si,fi] 和 [sj,fj ]互不重叠,ai 和aj 两个活动就可以被安排在这一天。该问题就是要安排这些活动使得尽量多的活动能不冲突的举行。
思路
该题似乎子问题的解的最优可以推出全局问题最优解,但是子问题之间是很难递推的,比如已知前 k 个活动的最优解,但是推 k + 1 个待安排活动的最优解很难推出来。
用贪心算法的思想如下:
- 将待活动按「结束」时间有小到大排序。
- 越早活动的「结束」时间最早,即为后面留下的时间区间更大。
- 依次比较排序后的「下一次活动的开始时间」与「上一次活动的结束时间」,如果能安排下(下一个开始时间「晚于」上一个结束时间)就将其放入安排数组里面。
- 按上一步对排序后的数组所有元素进行遍历,最终求出所有能安排的数组,长度即为所安排的最优活动个数。
实现
/**
* 贪心算法[1]-教室安排问题
*
* @author ychost
* @date 2018-4-2
*/
public class ArrangeRoom {
public static int greedySelector(Activity[] activities) {
List<Activity> list = Arrays.asList(activities);
list.sort(Comparator.comparingInt(a -> a.end));
int count = 1, j = 0;
for (int i = 1; i < list.size(); i++) {
//下一个活动的开始时间比上一个活动的结束时间晚,即可以安排下一个活动
if (list.get(i).start >= list.get(j).end) {
list.get(i).isSelect = true;
j = i;
count += 1;
}
}
return count;
}
}
class Activity {
public int start;
public int end;
public boolean isSelect;
public Activity(int start, int end) {
this.start = start;
this.end = end;
}
}
测试
@Test
public void greedySelector() {
int[] start = new int[]{1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12};
int[] end = new int[]{4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14};
Activity[] activities = new Activity[start.length];
for (int i = 0; i < start.length; i++) {
activities[i] = new Activity(start[i], end[i]);
}
swap(activities, 0, 1);
swap(activities, 5, 6);
swap(activities, 3, 4);
System.out.println(ArrangeRoom.greedySelector(activities));
}
void swap(Activity[] activities, int i, int j) {
Activity tmp = activities[i];
activities[i] = activities[j];
activities[j] = tmp;
}
//output
//4