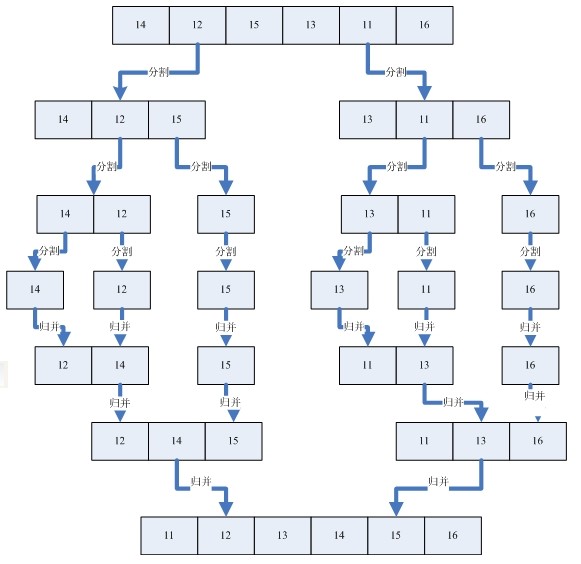
- 算法可视化：连接
- 时间复杂度，平均：\(O(nlogn)\)，最好：\(O(nlogn)\)，最坏：\(O(nlogn)\)
- 空间复杂度，\(O(n)\)
- 是否稳定：稳定
- 图片来源：https://www.cnblogs.com/of-fanruice/p/7678801.html
算法思想
- 归并排序采用的是「分治思想」
- 分解，把 n 个元素分解成两个子序列，每个子序列 n/2 个元素
- 治理，对每个子序列递归调用
MergeSort - 合并，合并两个排序好的子序列，生成排序结果
治理
void mergeSort(int[] array,int low, int high){
if(low < high){
int mid = (low + high) /2;
//分解与治理
mergeSort(array,low,mid);
mergeSort(array,mid+1,high);
//合并
merge(array,low,mid,high);
}
}
合并
对于两个有序的数列的合并，这里设 array[low..mid] 与 array[mid+1,high] 分别各自有序。
比如 4 7 9 1 5 8
array[low..mid] = 4 7 9
array[mid+1..high]=1 5 8。
- 令两个指针 p1 与 p2 分别指向 low 与 mid+1，暂存数组 tmp 与暂存数组指针 p
- 比较两个指向元素的大小，将较小的元素放入暂存数组，同时较小指针向右移动一位，暂存数组指针 p 向右移动一位
- 当比较完成之后将 p1 或者 p2 后面剩余的元素放入暂存数组
void merge(int[] array,int low,int mid,int high){
int[] tmp = new int[high-low+1];
int p1 = low,p2 = mid+1,p = 0;
while(p1<=mid && p2<=high){
if(array[p1] < array[p2]){
tmp[p++] = array[p1++];
}else{
tmp[p++] = array[p2++];
}
}
while(p1 <= mid){
tmp[p++] = array[p1++];
}
while(p2 <= high){
tmp[p++] = array[p2++];
}
//排序之后归位，覆盖未排序的元素
for(int i=0;i<p;i++){
array[low + i] = tmp[i];
}
}
实现
public class MergeSort {
public void sort(int[] array){
mergeSort(array,0,array.length-1);
}
void mergeSort(int[] array,int low,int high){
if(low < high){
int mid = (low+high)/2;
mergeSort(array,low,mid);
mergeSort(array,mid+1,high);
merge(array,low,mid,high);
}
}
void merge(int[] array,int low,int mid,int high){
int[] tmp = new int[high - low + 1];
int p1 = low, p2 = mid + 1, p = 0;
while(p1 <= mid && p2 <= high){
if(array[p1] < array[p2]){
tmp[p++] = array[p1++];
}else{
tmp[p++] = array[p2++];
}
}
while(p1 <= mid){
tmp[p++] = array[p1++];
}
while(p2 <= high){
tmp[p++] = array[p2++];
}
for(int i=0;i<p;i++){
array[low + i] = tmp[i];
}
}
}