背景
- 给定一个一维数组,求出两条边界的最大储水量值,Container With Most Water
Input: [1,8,6,2,5,4,8,3,7]
Output: 49
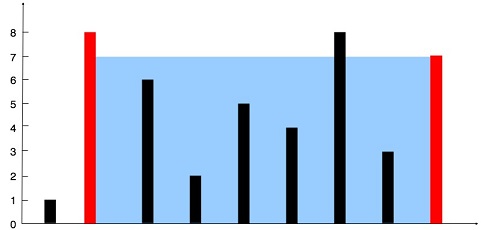
- 给定一个一维数组代表边界高度求最大的储水量,Trapping Rain Water
Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
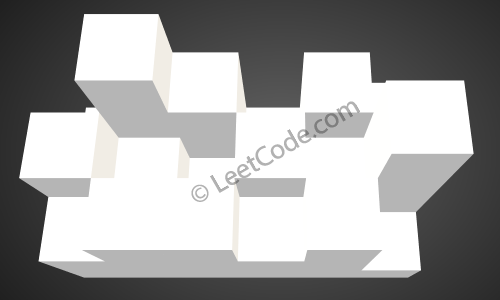
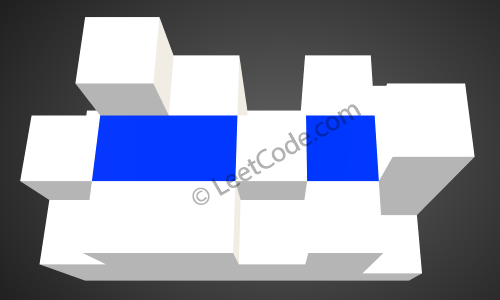
- 给定一个 mxn 的二维数组,求出其代表的容器的最大储水量,Trapping Rain Water II
Given the following 3x6 height map:
[
[1,4,3,1,3,2],
[3,2,1,3,2,4],
[2,3,3,2,3,1]
]
Return 4.
算法
两条边界储水量
该题可用双指针法求解,每次保留高度较高的那边,计算的时候按短边计算,详情参考 Solution
public int maxArea(int[] height) {
if(height == null || height.length < 2){
return 0;
}
int ans =0,l=0,r=height.length-1;
while (l<r){
// 短边法,找到 i,j 的储水量,更新最大值
ans = Math.max(ans,Math.min(height[l],height[r]) * (r-l));
// 保留长边,下次迭代
if(height[r] > height[l]){
l++;
}else{
r--;
}
}
return ans;
}
一维数组储水量
该题用动态规划比较好理解,详情参考 Solution
public int trap2(int[] heights){
if(heights == null || heights.length == 0){
return 0;
}
int[] leftMax = new int[heights.length];
int[] rightMax = new int[heights.length];
leftMax[0] = heights[0];
rightMax[heights.length-1] = heights[heights.length-1];
for(int i=1;i<heights.length;i++){
// i 左边的最大边界
leftMax[i] = Math.max(leftMax[i-1],heights[i]);
}
for(int j=heights.length-2;j>=0;j--){
// j 右边的最大边界
rightMax[j] = Math.max(rightMax[j+1],heights[j]);
}
int ans = 0;
for (int i = 0; i < heights.length; i++) {
// 用至该边界能储水的最大边界,减去该边界占的空间,剩下的就是能够储水的空间
ans += Math.min(leftMax[i],rightMax[i]) - heights[i];
}
return ans;
}
二维数组储水量
该题用优先队列,详情参考 Solution
public class Solution {
int[][] next = { {1, 0}, {0, 1}, {-1, 0}, {0, -1}};
public int trapRainWater(int[][] heights) {
if (heights == null || heights.length == 0 || heights[0].length == 0) {
return 0;
}
boolean[][] mark = new boolean[heights.length][heights[0].length];
// int[],有三个值 i,j,高度
// o1[2]-o2[2] 高度作为比较维度
PriorityQueue<int[]> queue = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[2] - o2[2];
}
});
// 先把最外层圈放入队列
for (int i = 0; i < heights.length; i++) {
for (int j = 0; j < heights[i].length; j++) {
if (i == 0 || j == 0 || i == heights.length - 1
|| j == heights[i].length - 1) {
queue.add(new int[]{i, j, heights[i][j]});
mark[i][j]=true;
}
}
}
int sum = 0;
while (!queue.isEmpty()) {
int[] cell = queue.poll();
for (int k = 0; k < next.length; k++) {
int ti = cell[0] + next[k][0];
int tj = cell[1] + next[k][1];
if (ti < 0 || tj < 0 || ti >= heights.length
|| tj >= heights[0].length || mark[ti][tj]) {
continue;
}
// cell 是当前外围的最低点
// 由于是由外向内遍历的,所以当前点为墙,ti,tj 指向的是内部
// 计算储水量,然后累加
sum += Math.max(0, cell[2] - heights[ti][tj]);
mark[ti][tj] = true;
// 因为要缩小一圈围墙,所以要取较大值,才能顶掉里面的值
queue.add(new int[]{ti, tj, Math.max(cell[2], heights[ti][tj])});
}
}
return sum;
}
}