1996年,John Platt 发布一个称为 SMO(Sequential Minimal Optimization,序列最小优化)的强大算法,用于训练 SVM,该算法的核心思想是将原问题分解成多个小问题分别进行优化求解,即 SMO 算法是为了解决 SVM 中的优化目标函数。
本文对于 SMO 算法进行了非常详细的剖析,建议读者对里面的公式推导进行亲自的演算,本文需要 SVM 的相关基础,如果对于 SVM 不熟悉可以参考 支持向量机通俗导论(理解SVM的三层境界)。
优化目标
SVM 的优化目标函数:
\[\begin{split} \mathop{min}\limits_{\vec{\alpha}} \Psi(\vec{\alpha}) = \begin{cases} \underbrace{ min }_{\alpha} \frac{1}{2} \sum\limits_{i=1}^{N} \sum\limits_{j=1}^{N} \alpha_i\alpha_jy_iy_jK(x_i,x_j) - \sum\limits_{i=1}^{N}\alpha_i\\ s.t. \; \sum\limits_{i=1}^{N}\alpha_iy_i = 0 \\ 0 \le \alpha_i \le C \end{cases} \end{split}\tag{1-1}\]其中,\(x_i\) 表示样本特征
\(y_i\) 表示样本标签,且 \(y_i \in \{-1,1\}\)
\(\alpha_i\) 为要求解的参数
\(C\) 为惩罚系数(自己设定)
SMO 算法剖析
SMO 算法的基本思想是将原问题求解 \((\alpha_1,\alpha_2,...,\alpha_N)\) 这 \(N\) 个参数的问题分解成多个子二次规划的问题分别求解,每个子问题只需要求解其中的 2 个参数,每次通过启发式选择两个变量进行优化,不断循环,直到达到函数的最优值。
选择 \(\alpha_1\) \(\alpha_2\) 为变量
将 \(\Psi(\vec{\alpha})\) 中 \(\alpha_1,\alpha_2\) 视作变量,其余的 \(\alpha_i i=3,4,...,N\) 的参数视为常数,则原优化目标函数变换如下:
\[\begin{split} \begin{align*} min\Psi(\alpha_1,\alpha_2) =&\frac{1}{2}K_{11}\alpha_{1}^2y_1^2 + \frac{1}{2}K_{22}\alpha_{2}^2y_2^2 \\ & + \frac12K_{12}\alpha_1\alpha_2y_1y_2 + \frac12K_{21}\alpha_2\alpha_1y_2y_1 \\ & - (\alpha_1 + \alpha_2) + y_1v_1\alpha_1 + y_2v_2\alpha_2 + P \end{align*} \end{split}\tag{2-1}\]由于,\(y_i^2 = 1\),\(K_{ij}= K_{ji}\),化简可得:
\[\begin{split} \begin{align*} min\Psi(\alpha_1,\alpha_2) =&\frac12K_{11}\alpha_1^2 + \frac12K_{22}\alpha_2^2 + K_{12}\alpha_1\alpha_2y_1y_2\\ &-(\alpha_1 + \alpha_2) + y_1v_1\alpha_1 + y_2v_2\alpha_2 + P \end{align*} \end{split}\tag{2-2}\]其中,\(K_{ij}\) 为核函数
\(v_i = \sum\limits_{j=3}^{N} \alpha_jy_jK_{ij} = 0\)
\(P\) 为常数项
用 \(\alpha_2\) 表示 \(\alpha_1\)
由 \(\sum\limits_{i=1}^{N} \alpha_iy_i = 0\) 得:
\[\alpha_1y_1 + \alpha_2y_2 = - \sum\limits_{i=3}^{N} \alpha_iy_i = \zeta \tag{2-3}\]等式两边同时乘 \(y_1\) 可得:
\[\alpha_1 = (\zeta - y_2\alpha_2)y_1 \tag{2-4}\]将 (2-4) 代入到 (2-2) 可得:
\[\begin{align*} \Psi(\alpha_2) = &\frac12K_{11}(\zeta - \alpha_2y_2)^2y_1^2 + \frac12K_{22}\alpha_2^2 + K_{12}(\zeta - \alpha_2y_2)\alpha_2y_1^2y_2\\ & -(\zeta - \alpha_2y_2)y_1 - \alpha_2 + v_1(\zeta - \alpha_2y_2)y_1^2 + y_2v_2\alpha_2 + P \end{align*} \tag{2-5}\]化简可得:
\[\begin{align*} \Psi(\alpha_2) = & \frac12K_{11}(\zeta - \alpha_2y_2)^2 + \frac12K_{22}\alpha_2^2 + K_{12}(\zeta - \alpha_2y_2)\alpha_2y_2\\ & -(\zeta - \alpha_2y_2)y_1 - \alpha_2 + v_1(\zeta - \alpha_2y_2) + y_2v_2\alpha_2 + P \end{align*} \tag{2-6}\]对 \(\alpha_2\) 求极值
由 (2-6) 可知,现在目标函数只是关于 \(\alpha_2\) 的函数,对其求导并令它等于 0
\[\begin{align} \frac{\partial \Psi (\alpha_2)}{\partial \alpha_2}&=(K_{11}+K_{22}-2K_{12})\alpha_2-K_{11}\zeta y_2+K_{12}\zeta y_2\\ &\quad+y_1y_2-1-v_1y_2+v_2y_2\\ & =0 \end{align} \tag{2-7}\]SMO 的思想是一个迭代求解的思想,所以必须构造出 \(\alpha_2^{new}\) 与 \(\alpha_2^{old}\) 之间的关系,由 (2-3) 可知:
\[\alpha_1^{new}y_1 + \alpha_2^{new}y_2 = \alpha_1^{old}y_1 + \alpha_2^{old}y_2 = \zeta \tag{2-8}\]由
\[\begin{align*} &f(x) =\omega^T x + b = \sum_{i=1}^{N} \alpha_iy_iK_{ix} + b\\ &v_i = \sum\limits_{j=3}^{N}\alpha_jy_jK_{ij} \quad\quad i=1,2 \end{align*} \tag{2-9}\]可得
\[\begin{align*} v_1 = f(x_1) - \sum\limits_{j=1}^{2}\alpha_jy_jK_{1j} - b = f(x) - \alpha_1y_1K_{11} - \alpha_2y_2K_{12} - b \\ v_2 = f(x_2) - \sum\limits_{j=1}^{2}\alpha_jy_jK_{2j} - b = f(x) - \alpha_1y_1K_{21} - \alpha_2y_2K_{22} - b \end{align*} \tag{2-10}\]将等式 (2-7) 中的 \(\zeta\) 替换成 (2-8),\(v_i\) 替换成 (2-9),\(\alpha_2\) 表示待求值,为了和 (2-8) 中的 \(\alpha_2^{old}\) 区分则用 \(\alpha_2^{new}\) 表示:
\[\begin{align*} \frac{\partial \Psi (\alpha_2)}{\partial \alpha_2} = &(K_{11} + K_{22} -2K_{12})\alpha_2^{new} - K_{11}(\alpha_1^{old}y_1 + \alpha_2^{old}y_2)y_2\\ &+ K_{12}(\alpha_1^{old}y_1 + \alpha_2^{old}y_2)y_2 + y_1y_2 - 1\\ &- \left[f(x_1) - \alpha_1^{old}y_1K_{11} - \alpha_2^{old}y_2K_{12} - b\right]y_2 \\ &+ \left[f(x_2) - \alpha_1^{old}y_1K_{21} - \alpha_2^{old}y_2K_{22} - b\right]y_2 \\ &= 0 \end{align*} \tag{2-11}\]对 (2-11) 进行展开
\[\begin{align*} (k_{11} + K_{22} - 2K_{12})\alpha_2^{new} = & K_{11}\alpha_1^{old}y_1y_2 + K_{11}\alpha_2^{old}y_2^2 - K_{12}\alpha_1^{old}y_1y_2\\ & - K_{12}\alpha_2^{old}y_2^2 - y_1y_2 + 1 + f(x_1)y_2 - K_{11}\alpha_1^{old}y_1y_2 \\ & - K_{12}\alpha_2^{old}y_2^2 - by_2 - f(x_2)y_2 + K_{12}\alpha_1^{old}y_1y_2 \\ & + K_{22}\alpha_2^{old}y_2^2 + by_2 \end{align*} \tag{2-12}\]由 \(y_i^2 = 1\) 化简可得
\[\begin{align*} (K_{11}+K_{22}-2K_{12})\alpha_2^{new}=&(K_{11}+K_{22}-2K_{12})\alpha_2^{old}\\ & +y_2\left[(f(x_1) - y_1) - (f(x_2) - y_2)\right] \end{align*}\tag{2-13}\]令 \(Ei = f(x_i) - y_i\),\(\eta = K_{11} + K_{22} - 2K_{12}\),可得
\[\alpha_2^{new}=\alpha_2^{old}+\frac{y_2(E_1-E_2)}{\eta} \tag{2-14}\]其中,\(\alpha_2^{new}\) 表示本次迭代的计算值,\(\alpha_2^{old}\) 为上一次的迭代值
\(E_i = f(x_i) - y_i\) 表示预测值与真实值的差
\(\eta=K_{11}+K_{22}-2K_{12}\)
\(\alpha_2^{new}\) 的约束
上面通过求导的方式计算出的 \(\alpha_2^{new}\) 是未经过约束的,即计算出来的值可能不满足约定的条件
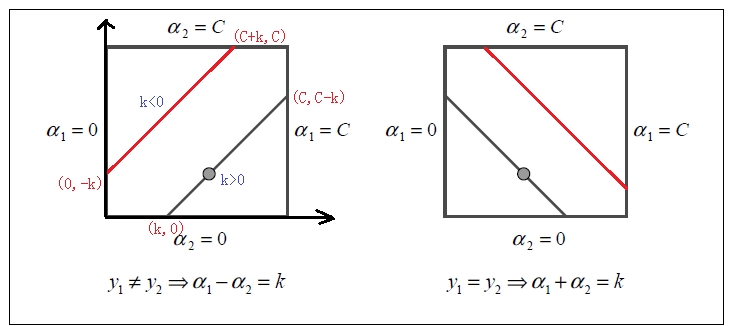
\[\begin{cases} 0 \le \alpha_i \le C \\ \alpha_1y_1 + \alpha_2y_2 = \zeta \end{cases}\tag{2-15}\]这两个约束条件可以在二维平面上进行直观的展示
上图横坐标为 \(\alpha_1\),纵坐标为 \(\alpha_2\),\(\alpha_2^{new}\) 必须要在方框内和斜线上取值,其最大最小值一定是其交点,所以有 \(L \le \alpha_2^{new} \le H\)
- 当 \(y_1 \ne y_2\) 时,\(L = max\left(0,\alpha_2^{old} - \alpha_1^{old}\right)\);\(H = min\left(C,C+\alpha_2^{old} - \alpha_1^{old}\right)\)
- 当 \(y_1 = y_2\) 时,\(L = max\left(0, \alpha_1^{old} + \alpha_2^{old} - C\right)\);\(H = min\left(C,\alpha_2^{old} + \alpha_1^{old}\right)\)
所以 \(\alpha_2^{new}\) 的约束如下:
\[\alpha_2^{new} = \begin{cases} H, \alpha_2^{new,unc} > H\\ \alpha_2^{new,unc}, L \le \alpha_2^{new,unc} \le H \\ L, \alpha_2^{new,unc} < L \end{cases} \tag{2-16}\]其中,\(\alpha_2^{new,unc}\) 表示 \(\alpha_2^{new}\) 未经约束的结果(上述通过求导的结果)
求解 \(\alpha_1^{new}\)
由公式 (2-8) 可知
\[\alpha_1^{new} = \alpha_1^{old} + y_1y_2(\alpha_2^{old} - \alpha_2^{new}) \tag{2-17}\]至此,通过公式 (2-14),(2-16),(2-17) 可以接出 \(\alpha_1^{new}\) 和 \(\alpha_2^{new}\),SMO 算法的核心逻辑已介绍完毕,后面将介绍如何选取变量 \(\alpha_1\) 和 \(\alpha_2\) 以及对 SVM 优化目标中的 \(b\) 求值。
SMO 变量选取
第一个变量选择
第一个变量的选择称为外循环,首先遍历整个样本然后选择违反 KKT 条件的 \(\alpha_i\) 作为第一个变量,其 KKT 条件如下:
\[\begin{aligned} \alpha_{i}=0 & \Rightarrow y_i\left(w^{T} x_i+b\right) \geq 1 \\ \alpha_{i}=C & \Rightarrow y_i\left(w^{T} x_i+b\right) \leq 1 \\ 0<\alpha_{i}<C & \Rightarrow y_i\left(w^{T} x_i+b\right)=1 \end{aligned}\]一般而言,首选选择违反 \(0<\alpha_{i}<C \Rightarrow y_i\left(w^{T} x_i+b\right)=1\) 这个条件点
如果支持向量都满足 KKT 条件,再选择 \(\alpha_{i}=0 \Rightarrow y_i\left(w^{T} x_i+b\right) \geq 1\) 和 \(\alpha_{i}=C \Rightarrow y_i\left(w^{T} x_i+b\right) \leq 1\) 这两个条件点
第二个变量选择
第二个变量选择的过程为内循环,选择 \(|E_1 - E_2|\) 取得最大值的 \(\alpha_2\)
如果内循环中找不到点能够使目标函数有足够的下降,则可遍历支持向量来做 \(\alpha_2\)
如果所有支持向量均不能使得目标函数有足够的下降,则跳出循环,重新选择 \(\alpha_1\)
SMO 阈值 \(b\) 的计算
1. 若 \(0 < \alpha_1^{new} < C\),则
由 \(y_1 = \left(\omega^Tx_1 + b\right) = \sum_{i=1}^{N} K_{i1}\alpha_iy_i + b\) 得:
\[b_1^{new} = y_1 - \sum\limits_{i=3}^{N}K_{i1}\alpha_iy_i - K_{11}\alpha_1^{new}y_1 - K_{21}\alpha_2^{new}y_2\tag{4-1}\]而
\[\begin{align*} y_1 - \sum\limits_{i=3}^{N}K_{i1}\alpha_iy_i &= y_1 - f(x_1) + K_{11}\alpha_1^{old}y_1 + K_{21}\alpha_2^{old}y_2 + b^{old} \end{align*}\tag{4-2}\]将 (4-2) 代入到 (4-1) 得:
\[\begin{align*} b_1^{new} = & y_1 - f(x_1) + K_{11}\alpha_1^{old}y_1 + K_{21}\alpha_2^{old}y_2 + b^{old} \\ &- \alpha_1^{new}y_1K_{11} - \alpha_2^{new}y_2K_{21} \end{align*}\tag{4-3}\]由 \(E_i = f(x_i) - y_i\) 化简可得:
\[\begin{align*} b^{new} = b_{1}^{new}=-E_{1}-y_{1} K_{11}\left(\alpha_{1}^{new}-\alpha_{1}^{old}\right)-y_{2} K_{21}\left(\alpha_{2}^{new}-\alpha_{2}^{old}\right)+b^{old} \end{align*}\tag{4-4}\]2. 若 \(0 < \alpha_2^{new} < C\),则
\[b^{new} = b_{2}^{new}=-E_{2}-y_{1} K_{12}\left(\alpha_{1}^{new}-\alpha_{1}^{old}\right)-y_{2} K_{22}\left(\alpha_{2}^{new}-\alpha_{2}^{old}\right)+b^{old}\tag{4-5}\]3. 若同时满足 \(0 < \alpha_i^{new} < C\),则
\[b^{new} = b_1^{new} = b_2^{new}\tag{4-6}\]4. 若同时不满足 \(0 < \alpha_i^{new} < C\),则
\[b^{new} = \frac{b_1^{new} + b_2^{new}}{2} \tag{4-7}\]关于上述取值分析可参考:SMO算法在更新参数b过程中的疑问
至此,SMO 算法剖析完毕。
总结
输入是 N 个样本 \((x_1,y_1),(x_2,y_2),...,(x_n,y_n)\),其中 \(x_i\) 为输入特征,\(y_i\) 为样本分类(只能取 \(1\) 或者 \(-1\)),输出是近似解 \(\alpha\)
注:\(\alpha_i\) 并不是只能取 \(1\) 或 \(-1\)
求解步骤:
- 取初值 \(\alpha = 0,t=0\)
- 选择变量 \(\alpha_1^t\) 和 \(\alpha_2^t\),根据公式求解出 \(\alpha_2^{t+1}\)
- 利用 \(\alpha_1^{t+1}\) 和 \(\alpha_1^t,\alpha_2^t,\alpha_2^{t+1}\) 的关系求解出 \(\alpha_1^{t+1}\)
- 通过 \(\alpha_1^{t+1}\) 和 \(\alpha_2^{t+1}\) 的满足的 KKT 条件关系求出 \(b^{t+1}\)
- 检查 \(E_i\) 是否在允许的精度 \(e\) 之内
- 检查求出的 \(\alpha_1^{t+1}\) 和 \(\alpha_2^{t+1}\) 是否满足 KKT 条件
- 如果上面两个条件都满足则返回 \(\alpha_1^{t+1}\) 和 \(\alpha_2^{t+1}\),否则跳转到第 2 步
SMO 算法可以实现对 SVM 的目标函数的快速优化,其推导过程是十分复杂的,所以需要有耐心将它一一进行剖析,但是 SMO 的求解步骤是十分清晰的,下一步将通过代码实现 SMO 算法。