SMO 是解决 SVM 中目标函数优化的一个快速的算法,本文通过 Python 代码实现了该算法,通过将原算法公式和代码进行一一比对让读者更能理会整个算法原理和实现步骤。
如果对文中的相关公式不了解请参考另一篇理论文章 SMO 算法超详细解析
准备
本算法实现参考于《机器学习实战》,相关的数据资源请自行下载
本文是基于 Python 来实现的整个算法,且依赖于 numpy
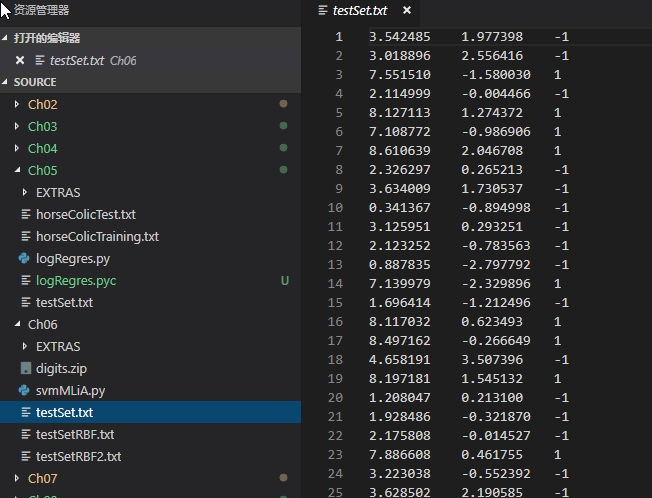
本文的测试数据集在 ch06 文件下面的几个 txt 文件,这些测试文件的数据都是标准的二分类数据
SMO 功能函数
加载数据
将上图中的 txt 测试数据加载到内存中,并生成指定的矩阵格式,其中特征数据赋值给了 X 矩阵,分类数据赋值给了 Y 矩阵
def loadDataSet(fileName):
"""
加载文本数据
:param fileName:
:return:
"""
X = []
Y = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
X.append([float(lineArr[0]), float(lineArr[1])])
Y.append(float(lineArr[2]))
# 分别转成矩阵,其中分类矩阵转置成一列
return mat(X), mat(Y).T
注入数据
将一些基础数据通过构造函数注入进行注入
class SMO:
def __init__(self, X, Y, C, e, gaussDelta=1.3):
"""
初始化构造函数,注入训练样本,常量,容错率
:param X: 样本特征
:param Y: 样本分类,只能取 {1,-1}
:param C: 常量
:param e: 容错率
:param gaussDetla: 高斯核函数的分母 delta 值
"""
self.X = X
self.Y = Y
self.C = C
self.tol = e
self.N = shape(X)[0]
self.alphas = mat(zeros((self.N, 1)))
self.b = 0
self.eCache = mat(zeros((self.N, 2)))
self.K = mat(zeros((self.N, self.N)))
for i in range(self.N):
self.K[:, i] = self.kernelGauss(self.X, self.X[i, :], gaussDelta)
高斯核
上述代码的最后有一行进行了高斯核处理,并将处理结果 \(K{ij}\) 进行了缓存:
\[K(x, y)=\exp \left(-\frac{\|x-y\|^{2}}{2 \sigma^{2}}\right)\tag{2-1}\]通过如下代码便可以实现高斯核,同时通过 calcKernel 方法直接返回了缓存的 \(K_{i,j}\) 结果
def kernelGauss(self, X, Y, delta):
"""
计算高斯核函数值
:param delta:
:return:
"""
m, n = shape(X)
k = mat(zeros((m, 1)))
for j in range(m):
diff = X[j, :] - Y
k[j] = diff * diff.T
return exp(-k / (2 * math.pow(delta, 2)))
def calcKernel(self, i, j):
"""
这里直接返回的之前缓存的核函数值
:param i:
:param j:
:return:
"""
return self.K[i, j]
计算 \(E_i\)
\(E_i\) 表示了预测值与真实值的差,其计算方法如下:
\[E_i = f(x_i) - y_i =\sum_{j=1}^{N} \alpha_{j} y_{j} K_{ij}+b - y_i\tag{2-2}\] def calcEi(self, i):
"""
计算 f(x_i) - y_i
:param i: 索引
:return: 预测值和真实值的差值
"""
aiyi = multiply(self.alphas, self.Y)
ki = self.K[:, i]
fxi = float(aiyi.T * ki) + self.b
ei = fxi - float(self.Y[i])
return ei
选择第二个变量 \(\alpha_j\)
由于第二个变量的选择比较麻烦,所以将其单独提取出来
def selectJ(self, i, ei):
"""
选择 |Ei - Ej| 取最大值的时候的 j,Ej,要求 Ej 是之前迭代的,否者返回随机选取的 j,Ej
:param i: 第一个变量
:param ei: 第一个变量的 Ei
:return: 第二个变量的 j,Ej
"""
j = -1
maxDeltaE = 0
ej = 0
self.eCache[i] = [1, ei]
# 要求选择的 Ej 必须是之前迭代过的,否则返回随机值
validEcacheList = nonzero(self.eCache[:, 0].A)[0]
if len(validEcacheList) > 0:
for k in validEcacheList:
if k == i:
continue
ek = self.calcEi(k)
deltaE = abs(ei - ek)
if deltaE > maxDeltaE:
maxDeltaE = deltaE
ej = ek
j = k
return j, ej
else:
j = self.selectJRand(i, self.N)
ej = self.calcEi(j)
return j, ej
def selectJRand(self, i, n):
"""
随机选择第二个变量
:param i:
:param n:
:return:
"""
j = i
while j == i:
j = int(random.uniform(0, n))
return j
def updateEi(self, i):
"""
更新 Ei 的缓存
:param i:
:return:
"""
ei = self.calcEi(i)
self.eCache[i] = [1, ei]
SMO 核心处理
\(\alpha\) 更新
\(\alpha_2\) 的更新
\[\alpha_2^{new,unc}=\alpha_2^{old}+\frac{y_2(E_1-E_2)}{\eta} \tag{2-3}\]其中,\(\alpha_2^{new}\) 表示本次迭代的计算值,\(\alpha_2^{old}\) 为上一次的迭代值
\(E_i = f(x_i) - y_i\) 表示预测值与真实值的差
\(\eta=K_{11}+K_{22}-2K_{12}\)
$$
代码实现,用 alphas[j] 表示 \(\alpha_2\)
eta = self.calcKernel(i, i) + self.calcKernel(j, j) - 2 * self.calcKernel(i, j)
ajOld = self.alphas[j].copy()
if self.Y[i] != self.Y[j]:
L = max(0, ajOld - aiOld)
H = min(self.C, self.C + ajOld - aiOld)
else:
L = max(0, aiOld + ajOld - self.C)
H = min(self.C, aiOld + ajOld)
self.alphas[j] = ajOld + self.Y[j] * (ei - ej) / eta
self.alphas[j] = self.truncateAlpha(self.alphas[j], H, L)
其中 self.truncateAlpha(self.alphas[j],H,L) 为 \(\alpha_j\) 的约束
def truncateAlpha(self, aj, H, L):
"""
对 Aj 进行截取,只能在 H L 之内
:param aj:
:param H:
:param L:
:return:
"""
if aj > H:
return H
elif aj < L:
return L
else:
return aj
\(\alpha_1\) 的更新
\(\alpha_{1}^{n e w}=\alpha_{1}^{o l d}+y_{1} y_{2}\left(\alpha_{2}^{o l d}-\alpha_{2}^{n e w}\right)\tag{2-5}\)
代码实现,用 alphas[i] 表示 \(\alpha_1\)
aiOld = self.alphas[i].copy()
self.alphas[i] = aiOld + self.Y[i] * self.Y[j] * (ajOld - self.alphas[j])
\(b\) 的更新
1. 若 \(0 < \alpha_1^{new} < C\),则
\[b^{new} = b_{1}^{new}=-E_{1}-y_{1} K_{11}\left(\alpha_{1}^{new}-\alpha_{1}^{old}\right)-y_{2} K_{21}\left(\alpha_{2}^{new}-\alpha_{2}^{old}\right)+b^{old}\tag{2-6}\]2. 若 \(0 < \alpha_2^{new} < C\),则
\[b^{new} = b_{2}^{new}=-E_{2}-y_{1} K_{12}\left(\alpha_{1}^{new}-\alpha_{1}^{old}\right)-y_{2} K_{22}\left(\alpha_{2}^{new}-\alpha_{2}^{old}\right)+b^{old}\tag{2-7}\]3. 若同时满足 \(0 < \alpha_i^{new} < C\),则
\[b^{new} = b_1^{new} = b_2^{new}\tag{2-8}\]4. 若同时不满足 \(0 < \alpha_i^{new} < C\),则
\[b^{new} = \frac{b_1^{new} + b_2^{new}}{2} \tag{2-9}\]代码实现
b1 = -ei - self.Y[i] * self.calcKernel(i, i) * (self.alphas[i] - aiOld) \
- self.Y[j] * self.calcKernel(j, i) * (self.alphas[j] - ajOld) + self.b
b2 = -ej - self.Y[j] * self.calcKernel(i, j) * (self.alphas[i] - aiOld) \
- self.Y[j] * self.calcKernel(j, j) * (self.alphas[j] - ajOld) + self.b
if 0 < self.alphas[j] < self.C:
self.b = b1
elif 0 < self.alphas[i] < self.C:
self.b = b2
else:
self.b = (b1 + b2) / 2.0
\(\alpha\) 和 \(b\) 更新代码
def updateAlphaB(self, i, e=0.00001):
"""
利用 SMO 算法优化一次 alpha_i, alpha_j, b
:param i: 训练样本索引
:param e: 最小更新步长
:return: 更新成功返回 1,失败返回 0
"""
ei = self.calcEi(i)
# 选择那些在容错率之外的样本作为第一个变量
if ((self.Y[i] * ei < -self.tol) and (self.alphas[i] < self.C)) or \
((self.Y[i] * ei > self.tol) and (self.alphas[i] > 0)):
j, ej = self.selectJ(i, ei)
aiOld = self.alphas[i].copy()
ajOld = self.alphas[j].copy()
if self.Y[i] != self.Y[j]:
L = max(0, ajOld - aiOld)
H = min(self.C, self.C + ajOld - aiOld)
else:
L = max(0, aiOld + ajOld - self.C)
H = min(self.C, aiOld + ajOld)
if L == H:
print("L == H")
return 0
eta = self.calcKernel(i, i) + self.calcKernel(j, j) - 2 * self.calcKernel(i, j)
# eta 类似于二阶导数值,只有当它 大于 0 才能取最小值
if eta <= 0:
print("eta <= 0")
return 0
# 计算 alpha_j 并截取在[H,L]之内
self.alphas[j] = ajOld + self.Y[j] * (ei - ej) / eta
self.alphas[j] = self.truncateAlpha(self.alphas[j], H, L)
self.updateEi(j)
if abs(self.alphas[j] - ajOld) < e:
print("j not moving enough")
return 0
self.alphas[i] = aiOld + self.Y[i] * self.Y[j] * (ajOld - self.alphas[j])
self.updateEi(i)
# 更新 b 的值
b1 = -ei - self.Y[i] * self.calcKernel(i, i) * (self.alphas[i] - aiOld) \
- self.Y[j] * self.calcKernel(j, i) * (self.alphas[j] - ajOld) + self.b
b2 = -ej - self.Y[j] * self.calcKernel(i, j) * (self.alphas[i] - aiOld) \
- self.Y[j] * self.calcKernel(j, j) * (self.alphas[j] - ajOld) + self.b
if 0 < self.alphas[j] < self.C:
self.b = b1
elif 0 < self.alphas[i] < self.C:
self.b = b2
else:
self.b = (b1 + b2) / 2.0
return 1
else:
return 0
训练样本
训练样本主要是从样本的非边界值和所有值来回进行选取
def train(self, maxIter):
"""
训练样本
:param maxIter: 最大迭代次数
:return: 训练好的 b,alphas
"""
iter = 0
entireSet = True
alphaPairsChanged = 0
# 在所有值和非边界值上面来回切换选取变量
while (iter < maxIter) and ((alphaPairsChanged > 0) or entireSet):
alphaPairsChanged = 0
# 遍历所有值,更新那些没有迭代过的数据
if entireSet:
for i in range(self.N):
alphaPairsChanged += self.updateAlphaB(i)
print("fullSet, iter: %d i: %d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
# 遍历非边界值
else:
# 在 alphas 中取出大于 0 小于 c 的索引值
# 即更新那些之前迭代过的 alpha_i alpha_j
nonBoundIs = nonzero((self.alphas.A > 0) * (self.alphas.A < self.C))[0]
for i in nonBoundIs:
alphaPairsChanged += self.updateAlphaB(i)
print("non-bound, iter: %d i: %d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
if entireSet:
entireSet = False
elif alphaPairsChanged == 0:
entireSet = True
print("iteration number: %d" % iter)
return self.b, self.alphas
样本测试
这里使用了两组样本,其中 testSetRBF.txt 为训练样本,testSetRBF2.txt 为测试样本
if __name__ == '__main__':
X, Y = loadDataSet("../source/ch06/testSetRBF.txt")
smo = SMO(X, Y, 200, 0.0001)
b, alphas = smo.train(10000)
# 支持向量即 alphas 大于 0 对应的那些有效的样本向量,这些向量是落在 SVM 的边界上面的
# 支持向量的索引
svIndices = nonzero(smo.alphas.A > 0)[0]
# 支持向量特征
xSv = X[svIndices]
# 支持向量分类
ySv = Y[svIndices]
print("there are %d Support Vectors" % shape(xSv)[0])
m, n = shape(X)
errorCount = 0
delta = 1.3
for i in range(m):
# 映射到核函数值
kernelEval = smo.kernelGauss(xSv, X[i, :], delta)
predict = kernelEval.T * multiply(ySv, smo.alphas[svIndices]) + b
if sign(predict) != sign(Y[i]):
errorCount += 1
# 训练样本误差
print("the training error rate is : %f" % (float(errorCount / m)))
errorCount = 0
X, Y = loadDataSet("../source/ch06/testSetRBF2.txt")
m, n = shape(X)
for i in range(m):
kernelEval = smo.kernelGauss(xSv, X[i, :], delta)
predict = kernelEval.T * multiply(ySv, smo.alphas[svIndices]) + b
if sign(predict) != sign(Y[i]):
errorCount += 1
# 测试样本误差
print("the test error rate is : %f" % (float(errorCount / m)))
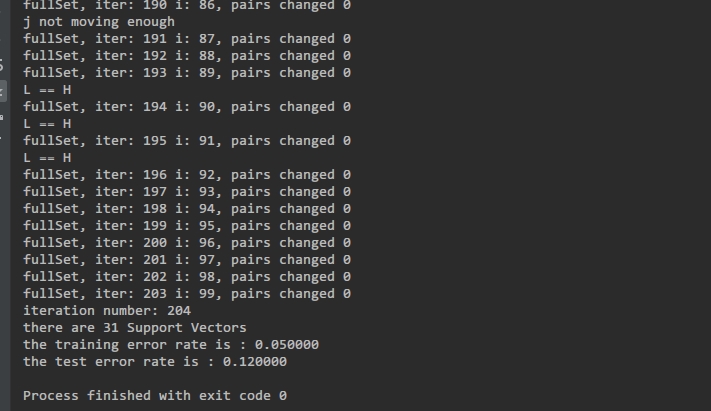
最终运行的效果截图
总结
SMO 算法的实现过程并不复杂,主要处理了核函数,变量\(\alpha_1,\alpha_2\)的选取,\(\alpha,b\) 的更新,样本训练的终止条件等问题
核函数主要使用了高斯核,当然也可以替换成其它的核函数。
\(\alpha_1\) 变量的选取是通过容错率 self.tol 来进行抉择的,主要选择那些在容错率范围之外的数据来作为 \(\alpha_1\)。
\(\alpha_2\) 变量的选取是当 \(|E_1 - E_2|\) 取最大值的时候对应的变量。
样本训练的终止条件通过最大迭代次数、更新是否成功、完整集训练等标志来确定的。
附录
完整代码
文件 smo.py
from numpy import *
class SMO:
def __init__(self, X, Y, C, e, gaussDelta=1.3):
"""
初始化构造函数,注入训练样本,常量,容错率
:param X: 样本特征
:param Y: 样本分类,只能取 {1,-1}
:param C: 常量
:param e: 容错率
"""
self.X = X
self.Y = Y
self.C = C
self.tol = e
self.N = shape(X)[0]
self.alphas = mat(zeros((self.N, 1)))
self.b = 0
self.eCache = mat(zeros((self.N, 2)))
self.K = mat(zeros((self.N, self.N)))
for i in range(self.N):
self.K[:, i] = self.kernelGauss(self.X, self.X[i, :], gaussDelta)
def calcEi(self, i):
"""
计算 f(x_i) - y_i
:param i: 索引
:return: 预测值和真实值的差值
"""
aiyi = multiply(self.alphas, self.Y)
ki = self.K[:, i]
fxi = float(aiyi.T * ki) + self.b
ei = fxi - float(self.Y[i])
return ei
def selectJ(self, i, ei):
"""
选择 |Ei - Ej| 取最大值的时候的 j,Ej,要求 Ej 是之前迭代的,否者返回随机选取的 j,Ej
:param i: 第一个变量
:param ei: 第一个变量的 Ei
:return: 第二个变量的 j,Ej
"""
j = -1
maxDeltaE = 0
ej = 0
self.eCache[i] = [1, ei]
validEcacheList = nonzero(self.eCache[:, 0].A)[0]
if len(validEcacheList) > 0:
for k in validEcacheList:
if k == i:
continue
ek = self.calcEi(k)
deltaE = abs(ei - ek)
if deltaE > maxDeltaE:
maxDeltaE = deltaE
ej = ek
j = k
return j, ej
else:
j = self.selectJRand(i, self.N)
ej = self.calcEi(j)
return j, ej
def selectJRand(self, i, n):
"""
随机选择第二个变量
:param i:
:param n:
:return:
"""
j = i
while j == i:
j = int(random.uniform(0, n))
return j
def updateEi(self, i):
"""
更新 Ei 的缓存
:param i:
:return:
"""
ei = self.calcEi(i)
self.eCache[i] = [1, ei]
def updateAlphaB(self, i, e=0.00001):
"""
利用 SMO 算法优化一次 alpha_i 和 alpha_j
:param i:
:param e:
:return:
"""
ei = self.calcEi(i)
# 选择那些在容错率之外的样本作为第一个变量
if ((self.Y[i] * ei < -self.tol) and (self.alphas[i] < self.C)) or \
((self.Y[i] * ei > self.tol) and (self.alphas[i] > 0)):
j, ej = self.selectJ(i, ei)
aiOld = self.alphas[i].copy()
ajOld = self.alphas[j].copy()
if self.Y[i] != self.Y[j]:
L = max(0, ajOld - aiOld)
H = min(self.C, self.C + ajOld - aiOld)
else:
L = max(0, aiOld + ajOld - self.C)
H = min(self.C, aiOld + ajOld)
if L == H:
print("L == H")
return 0
eta = self.calcKernel(i, i) + self.calcKernel(j, j) - 2 * self.calcKernel(i, j)
# eta 类似于二阶导数值,只有当它 大于 0 才能取最小值
if eta <= 0:
print("eta <= 0")
return 0
# 计算 alpha_j 并截取在[H,L]之内
self.alphas[j] = ajOld + self.Y[j] * (ei - ej) / eta
self.alphas[j] = self.truncateAlpha(self.alphas[j], H, L)
self.updateEi(j)
if abs(self.alphas[j] - ajOld) < e:
print("j not moving enough")
return 0
self.alphas[i] = aiOld + self.Y[i] * self.Y[j] * (ajOld - self.alphas[j])
self.updateEi(i)
# 更新 b 的值
b1 = -ei - self.Y[i] * self.calcKernel(i, i) * (self.alphas[i] - aiOld) \
- self.Y[j] * self.calcKernel(j, i) * (self.alphas[j] - ajOld) + self.b
b2 = -ej - self.Y[j] * self.calcKernel(i, j) * (self.alphas[i] - aiOld) \
- self.Y[j] * self.calcKernel(j, j) * (self.alphas[j] - ajOld) + self.b
if 0 < self.alphas[j] < self.C:
self.b = b1
elif 0 < self.alphas[i] < self.C:
self.b = b2
else:
self.b = (b1 + b2) / 2.0
return 1
else:
return 0
def truncateAlpha(self, aj, H, L):
"""
对 Aj 进行截取,只能在 H L 之内
:param aj:
:param H:
:param L:
:return:
"""
if aj > H:
return H
elif aj < L:
return L
else:
return aj
def calcKernel(self, i, j):
"""
这里直接返回的之前缓存的核函数值
:param i:
:param j:
:return:
"""
return self.K[i, j]
def kernelGauss(self, X, Y, delta):
"""
计算高斯核函数值
:param delta:
:return:
"""
m, n = shape(X)
k = mat(zeros((m, 1)))
for j in range(m):
diff = X[j, :] - Y
k[j] = diff * diff.T
return exp(-k / (2 * math.pow(delta, 2)))
def train(self, maxIter):
"""
训练样本
:param maxIter: 最大迭代次数
:return: 训练好的 b,alphas
"""
iter = 0
entireSet = True
alphaPairsChanged = 0
# 在所有值和非边界值上面来回切换选取变量
while (iter < maxIter) and ((alphaPairsChanged > 0) or entireSet):
alphaPairsChanged = 0
# 遍历所有值
if entireSet:
for i in range(self.N):
alphaPairsChanged += self.updateAlphaB(i)
print("fullSet, iter: %d i: %d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
# 遍历非边界值
else:
# 在 alphas 中取出大于 0 小于 c 的索引值
nonBoundIs = nonzero((self.alphas.A > 0) * (self.alphas.A < self.C))[0]
for i in nonBoundIs:
alphaPairsChanged += self.updateAlphaB(i)
print("non-bound, iter: %d i: %d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
if entireSet:
entireSet = False
elif alphaPairsChanged == 0:
entireSet = True
print("iteration number: %d" % iter)
return self.b, self.alphas
文件 test.py
from smo import *
from numpy import *
def loadDataSet(fileName):
"""
加载文本数据
:param fileName:
:return:
"""
X = []
Y = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
X.append([float(lineArr[0]), float(lineArr[1])])
Y.append(float(lineArr[2]))
# 分别转成矩阵,其中分类矩阵转置成一列
return mat(X), mat(Y).T
if __name__ == '__main__':
X, Y = loadDataSet("../source/ch06/testSetRBF.txt")
smo = SMO(X, Y, 200, 0.0001)
b, alphas = smo.train(10000)
# 支持向量的索引
svIndices = nonzero(smo.alphas.A > 0)[0]
# 支持向量特征
xSv = X[svIndices]
# 支持向量分类
ySv = Y[svIndices]
print("there are %d Support Vectors" % shape(xSv)[0])
m, n = shape(X)
errorCount = 0
delta = 1.3
for i in range(m):
# 映射到核函数值
kernelEval = smo.kernelGauss(xSv, X[i, :], delta)
predict = kernelEval.T * multiply(ySv, smo.alphas[svIndices]) + b
if sign(predict) != sign(Y[i]):
errorCount += 1
# 训练样本误差
print("the training error rate is : %f" % (float(errorCount / m)))
errorCount = 0
X, Y = loadDataSet("../source/ch06/testSetRBF2.txt")
m, n = shape(X)
for i in range(m):
kernelEval = smo.kernelGauss(xSv, X[i, :], delta)
predict = kernelEval.T * multiply(ySv, smo.alphas[svIndices]) + b
if sign(predict) != sign(Y[i]):
errorCount += 1
# 测试样本误差
print("the test error rate is : %f" % (float(errorCount / m)))