决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干,故称决策树。在机器学习中,决策树是一个预测模型,他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度,使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。
决策树最经典的算法包括:ID3、C4.5以及CART算法,ID3与C4.5算法相似,C4.5在特征选择时选用的信息准则是信息增益比,而ID3用的是信息增益;因为信息增益偏向于选择具有较多可能取值的特征(例如,某一特征具有5个可能取值,其信息增益会比具有2个特征取值的信息增益大)。
准备
信息熵
熵表示随机变量的不确定性,熵值越大表示随机变量含有的信息越少,变量的不确定性越大。
熵也是一个物理量和质量、温度、速度一样都是可以测定的,物理量的测定是需要参考物的,比如当测某个物体的质量时只需要计算该物体的重量为参考物的多少倍即可,比如参考物是 1KG,该物体的重量是它的 3 倍,那么该物体的质量为 3KG。
熵的测定也是一样的,不过熵表示不确定性那么选择的参考物为抛 1 个硬币(熵为 1)这种只有 2 种情况的不确定性,但是测量熵不是通过乘法来做的而是通过指数测量的,比如抛 3 个硬币(熵为 3)的情况不是 6 种而是 \(2^3 = 8\) 种,它的熵为 \(log_2{8} = 3\),再比如某个选择题的答案为 A B C D 中的一个,那么该题的熵为 \(log_2{4} = 2\)。即熵的一般公式为:
\[log_2{m}\]注:m 表示事件的不确定个数
当事件为非等概率的时候,其每个事件的不确定个数为概率的倒数
\[l(x_i) = log_2{\frac{1}{p(x_i)}} = - log_2{p(x_i)}\]注:这里的 \(\frac{1}{p(x_i)}\) 表示 \(x_i\) 的不确定个数
所以,样本集合的熵的计算公式如下:
\[H = - \sum_{i=1}^{n}{p(x_i)log_2{p(x_i)}}\]\(p(x_i)\) 表示 \(x_i\) 在总样本中的概率,熵的单位是 bit(比特)
关于熵解释还可以参考知乎 信息熵是什么?
信息增益
信息增益在决策树算法中是用来选择特征的指标,信息增益越大,则这个特征的选择性越好,在概率中定义为:待分类的集合的熵和选定某个特征的条件熵之差(这里只的是经验熵或经验条件熵,由于真正的熵并不知道,是根据样本计算出来的),公式如下:
\[IG(X|Y) = H(Y) - H(Y|X)\]信息增益就是 (含所有特征的熵 — 缺少某特征的熵)
决策树
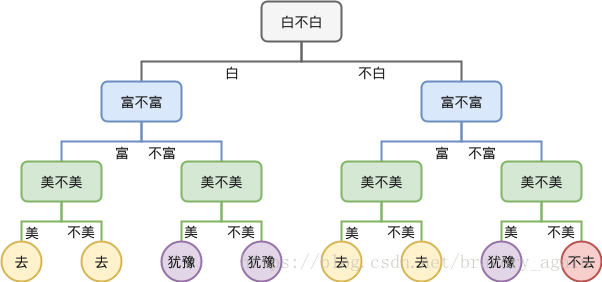
决策树的结构是一个树状的,每一节点都是一个决策点,通过做不同的决策可以将样本分到最终叶子点的不同分类里面去,比如下图所示的一个要不要去约会的决策判断
ID3 实现
计算信息熵
def calcEntropy(dataSet):
"""
:param dataSet: 样本集合,最后一列为分类数据
:return: 分类数据的信息熵
"""
labelsCount = {}
for line in dataSet:
# 分类标签
label = line[-1]
labelsCount[label] = labelsCount.get(label, 0) + 1
entroy = 0.0
for key in labelsCount:
# 计算熵
p = float(labelsCount[key]) / len(dataSet)
entroy -= p * math.log(p, 2)
return entroy
划分数据集
def splitDataSet(dataSet, index, value):
"""
删除样本的指定列
:param dataSet: 输入样本
:param index: 列序号
:param value: 样本中的列特征值等于 value 才有效
:return: 取出样本中指定列特征等于 value 的所有样本,且删除掉指定的列
"""
result = []
for feats in dataSet:
if feats[index] == value:
feat = feats[:index]
feat.extend(feats[index + 1:])
result.append(feat)
return result
选择最好的划分方式
def chooseBestFeat(dataSet):
"""
选择合适的特征列作为样本的划分标准,该特征为区分样本的最好的特征
:param dataSet: 样本集合
:return: 特征列序号
"""
# 最后一列为分类信息,不是特征
featuresCount = len(dataSet[0]) - 1
# 整体的信息熵
entropy = calcEntropy(dataSet)
bestInfoGain = 0.0
bestFeature = -1
for i in range(featuresCount):
# 样本的某一列
featVals = [ex[i] for ex in dataSet]
# 过滤掉重复值
uniquVals = set(featVals)
subEntropy = 0.0
for value in uniquVals:
# 切分样本
subDataSet = splitDataSet(dataSet, i, value)
# 计算切分后的信息熵
p = len(subDataSet) / float(len(dataSet))
subEntropy += p * calcEntropy(subDataSet)
# 整体的信息熵 - 子样本的信息熵
# 差值越大说明信息增益越大
infoGain = entropy - subEntropy
if infoGain > bestInfoGain:
bestInfoGain = infoGain
bestFeature = i
return bestFeature
简单的决策树
def classify(inputTree, featLabels, testVec):
"""
一个简单的决策树抉择
:param inputTree: 决策树的结构,该结构为手动实现,通过上述的划分特征来获取各个决策点
:param featLabels: 每个特征的名字
:param testVec: 测试样本
:return: 测试样本所属的分类
"""
key = inputTree.keys()[0]
root = inputTree[key]
# 当前测试的特征
featIndex = featLabels.index(key)
classLabel = -1
for k in root.keys():
# 抉择分类
if testVec[featIndex] == k:
# 决策点
if type(root).__name__ == "dict":
classLabel = classify(root[k], featLabels, testVec)
# 终结点
else:
classLabel = root[k]
return classLabel
总结
决策树分类就是一个带有终止块的流程图,终止块代表了分类结果。处理数据时根据信息增益来找到最好的划分数据的方式,直到将所有同一类数据划分到一起为止,然后可以通过递归的方式来判断出测试数据所属的分类。